Stepwise linear regression is a method of regressing multiple variables while simultaneously removing those that aren't important. This webpage will take you through doing this in SPSS.
Stepwise regression essentially does multiple regression a number of times, each time removing the weakest correlated variable. At the end you are left with the variables that explain the distribution best. The only requirements are that the data is normally distributed (or rather, that the residuals are), and that there is no correlation between the independent variables (known as collinearity).
Once you have your file in SPSS, pick the following menu item...

This should bring up the following dialog box...
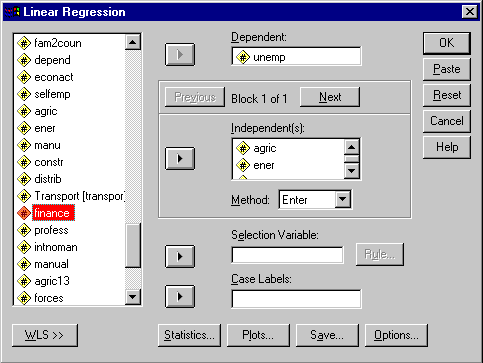
Pick your dependent and indepenent variables. To pick the variables you want to generate the statistics for, select them in the left side of the dialog box (example hightlighted red above), and click the arrow button in the middle of the dialog box to shift them into the various boxes. You can select several variables at once using the "shift" and "control (Ctrl)" keys. You can shift variables out of the boxes using the reverse procedure.
If you click on the "Statistics" button, you should get the following dialog box...
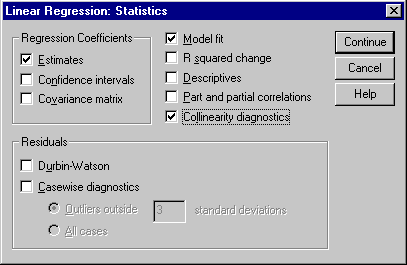
This allows you to generate several statistics. The most important in this context is the "Collinearity diagnositics". Ensure this box is ticked and push "Continue" to get back to the first dialog.
In the "Method" list, choose "Stepwise"...
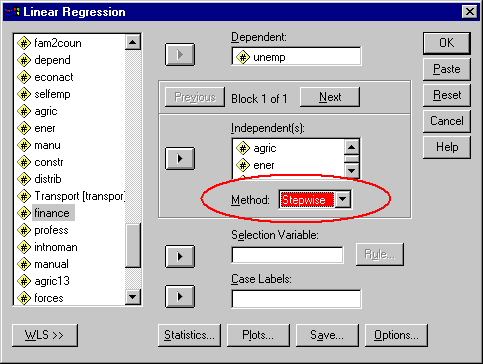
And then press "Ok" to run the analysis. After a short delay, the results viewer should appear. This shows various statistics for each "model". The models are composed of different sets of the variables. These models are the combinations of variables that best explain the dependent variable.
The first box should be the "Variables Entered / Removed" (if it isn't you should be able to pick it in the left hand frame/window). This shows the variables used to build the models.
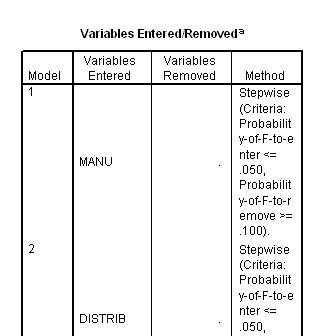
The next should be the "Model Summary" which gives details of the overall correlation between the variables left in the models and the dependent variable. With model 5 below, some 7 percent of the variation in the dependent variable can be explained using the independent variables listed below the box as "e".
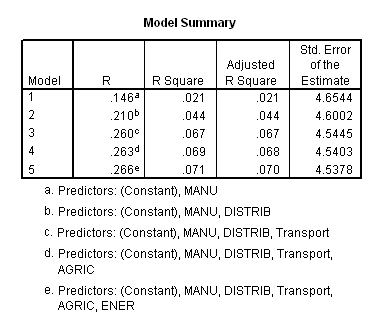
There should also be a Coefficients box, showing the linear regression equation coefficients for the various model variables. The "B" values are the coefficients for each variable, that is, they are the value which the variable's data should be multiplied by in the final linear equation we might use to predict long term illness with. The "Constant" is the intercept equilivant in the equation (i.e. the equation would be y = constant + (v1 x coeff1) + (v2 x coeff2) + ...). The Significance (Sig.) figures should be 0.05 or below to be significant at 95 percent. A value of .000 means the figure is too small for three decimal place representation.
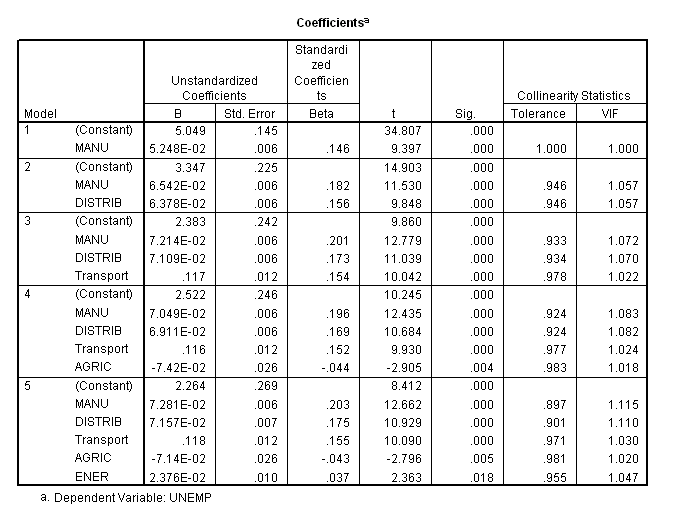
There should also be an "Excluded Variables" box showing the variables removed from each model.
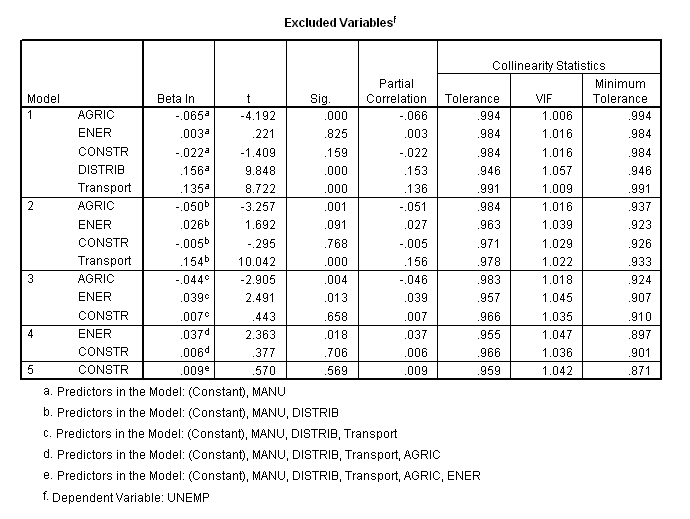
Finally there should be a "Collinearity Diagnostics" box, if you picked to have this shown.
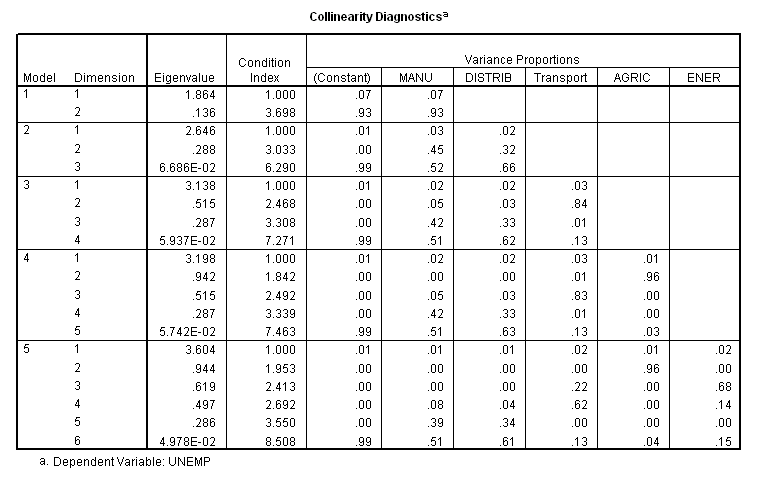
This gives you details of how the variables vary with each other. When two or more of the supposedly independent variables are correlated, the condition index for each will be above one. Values of one are independent, values of greater than 15 suggest there may be a problem, while values of above 30 are highly dubious. If the variables are correlated, one of the variables should be dropped and the analysis repeated. You can find more information on assessing collinearity here.
If you find collinearity is a problem in your data (i.e. it is not obvious that two collinear variables are related in the real world so you feel obliged to keep both), you can do a Principle Components analysis to get around breaking the necessary data rules. Principle Components analysis will regroup collinear variables into a single variable which can be used in techniques that require non-collinear data. You can run the stepwise linear regression using Principle Component groups to then cut out those groups which are not important. For more information see Principal Components Analysis (note that the PCA page was written by previous students - it will talk you though the basics, but there may be better ways of doing parts of it!).