 (2)
(2)
Stan Openshaw and Liang Rao
School of Geography, Leeds University, Leeds LS2 9JT
The availability of GIS technology and digital boundaries of census output areas now make it possible for users to design their own census geography. The paper describes three algorithms that can be used for this purpose. It briefly outlines an Arc/Info implementation and then presents case studies to demonstrate the usefulness of explicitly designing zoning systems for use with 1991 census data.
The 1991 census is the first UK census for which there is available a complete national set of digital boundary data with full topology for the smallest geographic areas used to report census statistics. In England and Wales there is now a highly accurate digital boundary database for census enumeration districts (eds); in Scotland digital boundaries are available for the equivalent census output areas. Previously, digital boundaries suitable for use with census data were only available for much larger geographical unit; for example, Districts in the 1970s wards and down to postcode sectors by the late 1980s. Sadly, none of the larger areal units are sufficiently small to be used as building blocks in zone design applications although quite adequate for census cartography purposes. The 1991 small area boundary data files present the first real opportunity that census users have had to build their own census geographies from the smallest possible building blocks. Of course, it is now easy via GIS to take small area digital boundaries and re-aggregate them to whatever higher level of census geography is considered relevant; for example, from eds to wards to districts to counties; see Carver, Charlton, and Rao, (1994). However, much more importantly the user is no longer restricted to a fixed census geography of eds or Wards or Districts or Counties. The census user can now design or engineer whatever spatial zoning systems are considered most suitable for a given purpose using spatial building blocks which are small enough to make the exercise worthwhile.
The case for analysing census variables for fixed sets of ward or district units was historically based mainly on convenience and feasibility rather than because Wards or Districts are considered to be the best or most meaningful geographical objects to study. For some purposes, these are sensible geographical objects; for example, Districts are obviously useful for studying processes that reflect the functioning of local authorities. However, the use of districts or wards to study geographical patterns in many census variables, such as unemployment or car ownership, is much more problematical. In the former, unemployment reflects the spatial organisation of the local economy which may be independent of local government boundaries. In the latter case, the underlying processes probably operates on a much more local scale, perhaps at a neighbourhood level and measures patterns and processes for which Districts and Wards are simply no longer sensible geographies. There is a grave danger of obtaining biased or misleading or poor results when data for possibly inappropriate areal units are studied. Once there was little or no choice, now there is.
It is to be observed that the purpose of analysing census data is often mainly descriptive rather than process related. The aim may be to either visualise the overall geographical distribution of a census variable or to rank areas by it as an area targeting device or to explore the data for spatial relationships. However, these activities immediate cause problems due to the likely sensitivity of the results to the scale and aggregation of the data being processed. This is the well known modifiable and unit problem (Kendall and Yule 1951; Openshaw, 1977a, 1977b, 1978a, 1978b, 1984 and Openshaw and Taylor 1979, 1981). However, the modifiable areal unit problem (MAUP) has recently become of much greater practical significance because the user is freed from having to use a limited number of fixed, usually "official" sets of areas for geographic analysis (Openshaw, 1989). The problem now is that of how best to exploit the new found freedom of user controlled zone design by developing sensible and appropriate zoning systems for particular purposes. It is noted that the recent rediscovery that different zoning system representations of the same data may or may not provide different results and that this or that statistic may be observed to vary for this or that artificial aggregation or when the zoning system is changed, is no longer surprising although still useful as a means of improving end user awareness; see Amrhein and Flowerdew (1992); Amrhein (1992) Fotheringham and Wong (1991). The principal value of such studies is to provide independent confirmation of the reality of the problem but without offering much prospect of a solution, with the limited exception of Arbia (1989).
A related geographical data problem that is much less well understood is the MAUP related spatial representation problem. There is an implicit assumption in mapping census data that the spatial variations in colour across the map are real and not largely an artefact of the mapping process. Monmonier (1991) points out how to adjust or fiddle the message being communicated by the map via careful selection of choropleth class intervals. Whilst interesting, this still ignores the wider spatial representation issue. The map is reporting in a cartographic form values for areal objects that need not be the same everywhere on the map and, indeed, seldom are. Census eds, Wards, and District entities vary in physical size, and they also vary in terms of the numbers of people they contain. This is well known. More important, however, is the observation that they also vary in the extent to which they represent one specific geographic object (a piece of space or zone) that is in some natural way comparable to other objects of the same logical type. The problem in geographical analysis is that data are reported for objects that are not basically the same, they are not strictly speaking comparable entities, and they have often no natural significance or innate meaningfulness.
Select any two census eds, have a close look at them and in particular at the areas and communities (or parts of community) they overlie and presumably try to represent. The key question is whether or not the ed boundaries make any sense in relation to the micro spatial patterns and process relevant to those small pieces of the earth's surface they represent. The problem is they seldom do. As Morphet (1993) argues "the only significant ed boundaries are those to be found between different but homogenous eds " (p1274) but then observed that ".. out of many thousand ed boundaries in the 1981 census map of Newcastle, only two, amounting to less than 200m of boundary length, are significantly located at the boundary of areas of different social composition" (p1276). Openshaw and Gillard (1978) in an even earlier study of boundary location in census classification noted that in their study region the only stable physical boundaries were located along railway lines.
From a geographical perspective most census areas are not natural nor comparable areal entities. More specifically, whilst Census eds do have some broad similarities; for instance, they have the same name (ie census eds) and they have been created by the same census geography planning process (ie they attempt to equalise the enumerators work load); they are also many differences. They vary in physical size; they vary in population size, they vary in terms of their internal socio-economic, demographic, and morphological heterogeneity, because they vary in terms of their ability to represent the underlying micro data. They are as like as chalk and cheese when viewed from a geographical perspective. They present one small area aggregated view of census data that varies enormously from one ed to another in terms of the amount of scale and aggregational noise, bias, and distortion they have added to the data. Of course all data aggregation procedures cause information loss and generalisation but the problem with census data is that the nature and extent of the loss of information is not consistent from one ed to the next, and it is also uncontrolled.
Few would claim that attempts to create eds that roughly equalise census enumerator workloads is a relevant zone design criteria for the spatial analysis of census data. Furthermore, the resultant census geography is arbitrary, highly non-random, and only one of many billions of possible alternatives. Faced with this problem, census analysts should be required to demonstrate that their particular results are meaningful, robust, and reliable given the vast amounts of aggregational uncertainty that typically seem to be present. If they use a standard fixed census geography, then they need to consider whether their results are representative of census data at that scale and capable of meaningful generalisation. If they design their own census geography, then they need to also consider whether they can justify their zone design criteria and how more representative they now consider their results to be. These are hard but fundamental problems that previously census analysts could ignore only because of their forced reliance on a small number of fixed spatial units precluded any attempt at identification or control.
Some of the spatial representation differences manifest themselves in spatially structured differences in the precision of the spatial census data. This can be regarded as small number problems that often make it easier for extreme values to appear in areas with small populations compared with areas that have much larger populations. It can be seen as differential data reliability due to sampling error in the 10% data. It can also be present in the averaging out of the individual census data records to create the spatial census data in the first place, when the averaging or data mixing process depends on the complex interaction between ed boundaries and underlying patterns of socio-economic homogeneity.
It is now much too late for the census agencies to redefine the 1991 census eds in order to provide a more consistent representation of the census microdata; although this could be done in 2001. The only remedial action open to the census user is to hope that by re-aggregating the ed data some of the worst problems can be avoided. The 1991 census presents the first real opportunity for users to re-engineer their census geographies to best suit their needs rather than have to rely on a small number of standard but arbitrary census geographies. The challenge is how best to do this efficiently and optimally.
Section 2 describes three algorithms designed to allow the census user to re-aggregate the 1991 small area census data into larger areal entities that are less arbitrary in terms of a specific purpose or application. Section 3 outlines the coupling of these methods to the Arc/Info GIS. Section 4 briefly presents some examples of use and Section 5 discusses possible future developments.
All the 1991 UK census data are reported for geographical objects. There is a standard hierarchy of geographies, whereby data at one scale nest into larger zones in the next level; see Denham (1993). The task here is to start with data at one scale and then re-aggregate it to create a new set of regions designed to be suitable for a specific purpose.
The zone design process involves the aggregation of spatial data for N zones into M regions, where M is less than N and usually a small fraction of N in size. The M output regions should be formed of internally connected, contiguous, subzones. Provided N is not too small, and M is not large in relation to N; there are many, many, billions of ways of aggregating N areas into M regions. The associated scale problem is much less binding and involves the selection of a suitable value for M. There are a maximum of N-2 choices and it is clear that the degree of scale induced variability will in general be considerably less than that caused by aggregational variability. Tobler and Moellering (1972) suggest that higher levels of generalisation (ie small values of M) might provide more explanation about the variance of a spatial variable than finer resolution levels. However, in general it would seem that scale is something that only needs to be broadly right whilst the aggregation needs to be optimised. These problems can be avoided only if acceptable frame independent spatial analysis and modelling procedures can be developed, see Tober (1989). The problem is that for census analysis frame independent methods might not make much geographical sense.
The earliest zone design procedures might be considered to be the regionalisation algorithms that were concerned with either the multivariate classification of data subject to a contiguity restriction or the functional regionalisation of flow data. Electoral redistricting might be considered another variant of the problem as indeed is location-allocation partitioning. Openshaw (1978, 1984) argued that these are all special cases of a more general zone design problem that was the geographers equivalent to a special type of non-linear optimisation problem in which the parameters to be optimised was the classification of N areas into M.
This can be stated as
optimise F(Z) (1)
subject to constraints on Z to ensure the M regions are internally connected, F(Z) is any function defined on data for the M regions in Z, and Z is the allocation of each of N zones to one of M regions such that each zone was assigned to only one region.
Unfortunately, there is no convenient general purpose mathematical programming representation of this problem. Also in general F(Z) would be nonlinear, discontinuous, and nondifferentiable in terms of Z since Z is not a set of parameters in the conventional sense but a zoning system. It is at best some kind of discrete integer nonlinear discontinuous programming problem that could well have many suboptima. The only general purpose solution strategy was likely to be some kind of combinatorial search heuristic.
The original automatic zoning procedure (AZP) of Openshaw (1977, 1978a, 1978b) was, a heuristic procedure that evolved by trial and error into a method suitable for solving the AZP in equation (1) from an iterative relocation method commonly used in numerical taxonomy. Subsequent work allowed the AZP to be solved with other constraints being enforced on the shape of the M regions and, or, on the aggregated data being generated by the zoning system. Openshaw (1979) gives examples of the fit of a linear regression being optimised subject to constraints that the residuals should have zero spatial autocorrelation and be homoscedastic.
In principle, once you can solve the unconstrained zone design problem the imposition of various other side conditions in the form of equality and inequality constraints can be handled via penalty function methods (Openshaw, 1978a, 1978b). The greatest practical difficulty is the choice of objective function, and that of deciding what constraints should be imposed on the data. Since in geographical analysis zone design, result, and pattern all interact, there is a risk of causing considerable damage to unknown spatial patterns by accident. The zoning system acts as a pattern detector and the nature of the patterns it detects depends on the function being optimised, and how this interacts with the data being represented by the set of M regions, as well as with any additional constraints imposed on the zoning system being estimated, on the size of M in relation to N, and on the size of N in relation to the data being represented by the N initial zones. Virtually all aspects of the interaction are currently dimly understood.
It is recommended, that initially at least, attention should be focused on the unconstrained zone design process; especially if the output regions are primarily of interest as a visualisation of the interactions between model or result and the data. Insisting that all the regions in M should be compact is often a requirement that owes more to aesthetics than any principle relevant to geographical analysis. If you "force" the M regions to be compact in shape or to yield normally distributed data; then this will constrain the search heuristic to consider solutions in a very different part of the universe of all possible, feasible, zoning systems. It can be done but maybe it is best left to future study when more is understood about the dynamics of simpler unconstrained zonings of spatial data.
The original Openshaw (1977, 1978a, 1978b) AZP algorithm is a fairly simple local boundary optimiser. It involves the following:
step 1 start by generating a random zoning system of N small zones into M regions, M<N.
step 2 make a list of the M regions
step 3 select and remove any region K at random from this list
step 4 identify a set of zones bordering on members of region K that could be moved into region K without destroying the internal contiguity of the donor region(s)
step 5 randomly sample this list until either there is a local improvement in the current value of the objective function or a move that is equivalently as good as the current best then make the move and return to step 4, else repeat step 5 until the list is exhausted
step 6 when the list for region K is exhausted return to step 3 and select another and repeat steps 4 to 6
step 7 Repeat steps 2 to 6 until no further improving moves are made.
This AZP algorithm can work with any type of objective function that is sensitive to the aggregation of data for N zones into M regions that is being evaluated in step 5. Examples included functions computed directly from the data, for example, sum of squared deviations from average zone size, and also functions which represent the goodness of fit of a model applied to the data; for example, the fit of a linear regression model or the performance of a spatial interaction model.
This generality is important because the underlying purpose in designing the AZP was threefold. First to identify the approximate limits of aggregation effects on any statistic, or model, by the simple expedient of first maximising and then minimising its performance on the same data. Second to demonstrate that the modifiable areal unit problem is endemic and affects all the results of studying spatially aggregated data and that, despite claims to the contrary, there are probably no geographically meaningful exceptions in the form of zoning system invariant spatial models. Finally to provide a basis for developing a new approach to the aggregation problem based on two principles. The first suggests that the estimation of the zoning system is the geographical equivalent to the estimation of parameters in a model. The second suggests that the zoning system that best fits a particular statistic or model provides a map visualisation of the interaction between data, model or statistic, and scale. It was conjectured that this might provide useful insights about pattern and process. Openshaw (1984) showed that a zoning system could often be manufactured to fit a model with its parameters fixed at some predefined values. This is the inverse of the normal parameter estimation process, in which a model's parameters would be manufactured to fit a predefined zoning system! In the former case, the configuration of the best fitting zoning system provides a spatial 'picture' of what is needed if the model is to fit the data. It offers a limited visualisation of the interaction between model, zoning system and data. It was suggested that this new form of spatial analysis by mapping optimal data aggregations might be useful in certain circumstances although until GIS existed it was virtually impossible to test on realistic data.
The AZP algorithm is not in the steepest descent direction because the search is local to a selected region. This is deliberate. A steepest descent version would scan the global list of all possible single moves that could be made for all M regions and then select the best. Surprisingly, this is much less effective than the basic AZP algorithm, and it is also considerably more expensive because of the much greater number of different zoning systems that would have to be evaluated before a move could be made. More serious is the observation that the steepest descent algorithm often gets struck, whereas the local optimiser follows a much more gradual route towards a local optimum and this seems to be much better suited to zone design problems. Furthermore, in the mid 1970s the greatly reduced compute times was a very important practical consideration for a method that was barely feasible at that time. However, the AZP method can also become stuck, although the usual solution of re-running the algorithm from a number of different randomly generated starting zonings and then select the best often works extremely well.
A number of empirical studies have used this AZP algorithm seemingly quite successfully; for example, Openshaw (1977, 1977b), Openshaw and Taylor (1979), and Openshaw (1978a). However, this work was restricted to fairly small data sets; Openshaw (1977) used 1,219 100m grid squares but this might be regarded as an "easy" set of building blocks to rezone because of their Queen's case contiguity regularity. Most of the other uses of the algorithm were on the gridsquare-like 99 Iowa Counties, aggregating to various numbers of regions down to 6 regions; on 73 zone spatial interaction journey to work data for Durham County (aggregating to 22 regions); and some unpublished political redistricting involving small numbers of zones and regions in Scotland.
A major problem in the pre-GIS 1970s, was the need to create the contiguity lists by hand and this tended to restrict the size of the data set that was experimented with. The grid square data was an exception because of the ease by which the contiguities could be generated automatically. Another difficulty concerned mapping the M regions that were produced at a time when the cartography was manual. GIS has removed both problems. It is observed however that the performance of the simple AZP algorithm seems to diminish as the N into M aggregation problem becomes harder due to both increasing N and also irregularities in zone size and shape; for example, compare census ed data with Districts. The availability of larger data sets causes other difficulties. The number of alternative ways of aggregating N zones into M regions explodes combinatorially as N increases. This greater aggregational freedom helps when N is not too big but then as N continues to increase it starts to reduce the efficiency of the algorithm as the number of local suboptima also rapidly increase. This combinatorial complexity and hardness of the optimisation task also interacts with the nature of the function being optimised. Some functions are hard to optimise; particularly those which are not model based; and the AZP method can converge too quickly at a poor result. Successive restarts from different random starts often works but is lacking in elegance. The imposition of other constraints via penalty function methods may also make failure more frequent.
The principle problem with AZP is that of being trapped by a local suboptimum which is not very good and which is starting zoning system dependent. There are ways of reducing this problem; for example, by extending the search process to consider two, three, or more moves at a time in the search for a local improvement. This greatly increases compute times although it has been successfully used to overcome the limitation of the basic AZP's single move heuristic in redistricting applications. The real question now with much faster computer hardware is whether or not a different heuristic might provide much better results.
A very widely used method in combinatorial optimisation is that of simulated annealing; see Aarts and Korst (1989). Simulated annealing sometimes called the Metropolis technique, was originally developed to solve a hard optimisation in physics (Metropolis et al, 1953). It has subsequently developed into a global optimisation method particularly suitable for problems with multiple suboptima; Kirkpatrick et al (1983). There have so far been few geographical applications of it; see Openshaw (1988). It is essentially a Monte Carlo optimisation procedure that can escape from local suboptima. It provides a robust optimisation for optimisation problems which are otherwise hard to solve. It is therefore inherently attractive as a potential AZP solution method.
The basic simulated annealing AZP method (AZP-SA) is simple to apply. The local search step 5 in AZP algorithm only need be modified as follows
step 5 randomly sample this list until there is a local improvement in the objective function or an equivalently good move then make the move, otherwise make the move with a probability given Boltzmann's equation
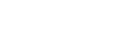 (2)
(2)
where f is the change in objective function due to the move,
T(k) the "temperature" at annealing time step k, and
R(0,1) is a uniformly distributed random number in the range 0.0 to 1.0.
The hardest part is determining a suitable slow annealing schedule with the temperature being lowered in a sufficiently large number of steps to ensure that a very good result has had sufficient time to emerge. There are some proofs that establish the global optimality of the simulated annealing method but these require a very gradual annealing process such that
T(k) = T(0)/ln(K) (3)
This is much slower that most algorithms which typically use an exponentially decreasing annealing schedule, viz
T(k) = T(k-1) *f (4)
where f is typically between 0.8 to 0.95 see for example, Press et al (1986).
The secret of the simulated annealing algorithm is that it permits moves which result in a worse value of the objective function but with a probability that diminishes gradually, through iteration time K. This means that the AZP-SA algorithm now has to be embedded in an iteration loop that slowly reduces T from some arbitrarily high initial value. The initial value of T(0) would be set such that about half of all moves would be accepted. It is important to ensure that the zoning system is properly 'melted' before applying an annealing and cooling schedule to it.
step a set T(0), K=0
step b apply AZP with the modified step 5 until either MAXIT iterations or convergence or at least a minimum of 200 simulated annealing moves have been made
step c update T and K
T(K) = T(K-1) * 0.85
step d repeat steps 2 and 3 until no further moves occur over at least 3 different K values.
It was soon realised that the local serial move heuristic used in AZP was now not necessary and was responsible for too much movement; indeed waves of change used to ripple through the zoning system. This might well be a useful feature but maybe there was considerable unnecessary movement that could be avoided.
The algorithm was changed to a steepest descent search in the single move neighbourhood of the current solution
step 5.0 make a list of all possible single moves for all regions
step 5.1 find best
step 5.2 accept an equivalent or improving move, else
step 5.3 accept a worse move with probability defined by equation (2)
step 5.4 go to step 5.0
This reduced the amount of movement although at the cost of a big jump in compute times. However, experience demonstrates that this method also produces what look like extremely good results. As computer hardware becomes faster so the about two to four orders of magnitude increase in compute times over the basic AZP method becomes insignificant.
Another relatively new heuristic that can be applied to zone design problems is tabu search, Glover (1977, 1986). This started out as an integer programming method but is now regarded as being suitable for a wide class of combinatorial optimisation problems which are NP hard; Glover and Laguna (1992), Hertz and de Werra (1987), Bland and Dawson (1991) The AZP is certainly of this form and any heuristic that is capable of generating near-optimal solutions to hard combinatorial problems which may have many different local optima is of potential interest here. Simulated annealing certainly meets these needs but it is computationally very expensive. The hope is expressed that tabu search might be quicker and almost or equivalently good.
A basic tabu version of the AZP is specified as follows
step 5.1 find the global best move that is not prohibited or tabu
step 5.2 make this move if it is an improvement or equivalent in value else
step 5.3 if no improving move can be made then see if a tabu move can be made which improves on the current local best (termed an aspiration move) else
step 5.4 if there is no improving move and no aspirational move then make the best move even if it is non-improving (ie results in a worse value of the objective function)
step 5.5. tabu the reverse move for R iterations
step 5.6 return to step 5.1
It is noted that both simulated annealing and tabu search define a search trajectory and it is necessary to retain the global best result information outside of the local best solution currently being found by the algorithm. They may coincide at the end of the process but do not have to. The tabu algorithm is a powerful optimisation tool that allows the search process to escape from local optima whilst avoiding cyclical behaviour. The only real requirement is that the list of possible moves is even in its coverage of the solution space, which it clearly is in the zone design context. The key algorithmic parameter is the length of tabu period R. If a zone I is moved from region K to region L then the reverse move is prohibited for R subsequent iterations. Clearly the value of R should not equal or exceed the number of possible moves. The purpose of tabu-ing reverse moves is to force the algorithm to look elsewhere for new or better results, even if it means making non-improving moves. This results in a very aggressive search process that is constantly trying to discover better results without repeating itself too much.
The aspirational criteria in step 5.3 is designed to allow the search to temporarily release a solution from its tabu status if it finds an improving solution. It seeks to improve the flexibility of the method. According to Glover (1977) the aspiration value for a given cost is the current lowest cost of all solutions arrived at from solutions with cost C. In a zone design context this is interpreted as being a better result than the current local best.
The principal practical problem with AZP-tabu search in a zone design context and elsewhere is defining a suitable tabu length for R. The results can critically depend on specifying a good value for R but seemingly there is no easy or good way to do this. It also seems to be problem specific. One solution that works well with zone design problems is to simply repeatedly rerun the method starting with a small R value and then steadily increasing it. Each tabu sub optimisation problem is then run to completion. This works very well especially when the best result is selected from a small number of different random starts.
A more pleasing solution to specifying a good R value is to adapt the reactive tabu search of Battiti and Tecciolli (1993, 1994) to AZP problems. This algorithm provides a more efficient exploration that becomes even more powerful the harder the problem becomes. It involves the following procedure:
step 1 start with random zoning system
step 2 set the length of prohibition (R=1) and the average number of iterations between repetitions (rav=1.0)
step 3 define the list of all possible moves that are not tabu and retain regional connectivity
step 4 find the best nontabu move
step 5 make the move, update the tabu status
step 6 look up the current zoning system in a list of all zoning systems visited so far during the search, if not found then go to step 10
step 7 if it is found and it has been visited more than K1 times already and this cyclical behaviour has been found on at least K2 other occasions (involving other zones) then go to step 11
step 8 update a moving average of the repetition interval rav, and increase the prohibition period R = R*1.1
step 9 if the number of iterations since R was last changed exceeds rav, then decrease R = max (R*0.9, 1)
step 10 save the zoning system and go to step 12
step 11 delete all stored zoning systems and make p random moves P = 1 + rav/2 and update tabu to preclude a return to the previous state
step 12 repeat steps 3 to 11 until either no further improvements are made or a maximum number of iterations are exceeded
The reactive tabu dynamically adjust the prohibition period R as the search proceeds. There is a memory mechanism that is used to prevent repeat results. Experiments indicate that there is no need to store the complete zoning system in step 6 as this can be easily simulated by storing the sum of the classification array and the objective function that results. If the same zoning system is repeated more than a small number of time (K1 = 3) by more than a small number of different regionalisations (K2 = 3) then a series of random moves are made and R is increased. The random moves are designed to escape from the neighbourhood of the current solution and the tabu is used to prohibit an early return there. In a zoning context the best strategy is to make P random moves for each of the M regions; see step 11. The avoidance of cycles is important in order to ensure that the available time is spent in an efficient exploration of the search space. The principal problem now is the potentially large number of iterations that may be needed.
There is seemingly much confusion at present about how best to develop parallel algorithms. Some believe that a clever parallelising compiler will miraculously convert serial code into parallel code. This certainly works to some extent. However, this is no substitute for designing an algorithm in such a way that most of the operations can be executed in an explicitly parallel fashion. An interesting property about many map related analysis and modelling tasks is that they are inherently and explicitly parallel; zone design is no exception. The hardest decision is knowing at what level of granularity to develop parallelisation at. This has historically been an issue related to the architecture of the intended parallel hardware. However, increasingly this is less of a problem and with the prospect of teraflop computing speeds on terabyte memory hardware during the late 1990s, it is becoming extremely worthwhile to develop parallel zone design algorithms.
Clearly the basic AZP algorithm as described in section 2.2 is not suitable for parallel implementation, although depending on the objective function being used, there may well be vectorisation opportunities. The AZP is not a parallel algorithm because of its local sequential search for improvements in the objective function. It could be transformed into one only by performing the local search in parallel on different parts of the map which are not contiguous provided the objective function was decomposable so that the contribution of any of the M regions to it could be examined and changed independently of all others. Surprisingly, this is often the case and the benefits of this form of parallel boundary optimisation increases with N. A particular attraction would be an ability to exploit any contiguity islands in the original N zone topology. A small zone national census data set might contain a hundred or so such totally separate islands and the zone optimisation task for each island could be safely allocated to a different processor.
Perhaps more important is the observation that both the simulated annealing and tabu search versions of AZP have a high degree of explicit parallelism in them. Both involve the repeated application of the following process:
step 1 make list of all possible single moves
step 2 check each possible move for contiguity violation
step 3 evaluate each move by computing a function for the new data that would be created by it
step 4 find a 'best' move
Steps 2 and 3 are capable of parallel execution, indeed the vast majority of the time spent in the simulated annealing and tabu search is here. Moreover, the more complex the objective function becomes so the parallel computer times will approach 100 per cent. If penalty function based constrained optimisation is required then the cost of evaluating the penalty function would also be included in parallel step 3. Additionally, the number of candidate moves to be evaluated rapidly exceeds the number of processors likely in most massively parallel machines; Table 1 provides illustrative sizes for the data sets analysed in Section 4. It is apparent that zone design problems could easily make very good use of multiprocessor systems with 256 or even 1024 processing nodes. As N increases so the amount of parallel activity increases. It is argued, therefore, that zone design can be regarded as being explicitly suitable for massively parallel hardware even though the current algorithms have not yet been run on any such machine. Research is underway to demonstrate scalability.
The algorithms described in section 2 are not standalone software. The AZP methods require contiguity information as inputs and then some means of mapping the resulting optimal aggregations. Neither task can be easily performed by hand, indeed this was one of the major unresolved problems faced by the early AZP work in the late 1970s. The availability of GIS software changes all this and also provides an ideal environment within which to engineer new zoning systems. It also offers a natural way of disseminating zone design tools in a form that GIS literate users can appreciate. This section describes the development of one such system called ZDES (Zone Design System).
The choice of GIS often seems to present major philosophical problems. Here there can only be one choice, that of Arc/Info. The reasons are as follows: it is a de facto worldwide standard, it operates on many different computer platforms, it has a large number of research users in Britain and many other countries, and there is nothing to preclude developing interfaces for other GISs if needed later. The AZP software is written in FORTRAN 77 and is GIS independent, only the interfacing is Arc/Info specific.
The objective is to develop a zone design system for Arc/Info within which the linkages between the GIS and AZP functions are completely transparent to the user and which would also permit the AZP optimisation to take place on a different machine from that with the GIS on it. What follows assumes Arc/Info version 6.1.1 (or higher) operated on UNIX workstations. Arc/Info provides a set of macro programming facilities (AML) for linking functions within and outside Arc/Info and also allows the users to build the menu-driven applications. Under OpenLook or Motif, sophisticated Graphic User Interfaces (GUI) can be easily created by using Arc/Info's THREAD-MENU-POPUP tools.
AZP requires a topologically "cleaned" data structure from which logically consistent inter-zone contiguities can be generated. In the Arc/Info data model, the relationships between spatial objects should be identifiable in a coverage. This provides an easy means of generating the contiguity table from any input zoning system or polygon coverage.
There are two Arc/Info methods for obtaining the contiguity matrix for a zoning system. The first is by reading the AAT. In a cleaned polygon coverage, every arc is shared by two polygons, so in its AAT there is a left and a right polygon. From this a contiguity table can be produced. The second method is by spatial query. In ARCPLOT, the RESELECT command performs a spatial query for identifying the "ADJACENT" polygons of any selected polygon. The query could also have a buffer distance. By changing this distance, the spatial contiguity association of zones no longer have to be restricted to strictly physically map based contiguities. A much more flexible definition of contiguity can be used, one that is able to bridge holes in the physical map topology due to barriers; for example, a river.
The AZP algorithms described in Section 2 are general purpose in that they can approximately optimise any function with a value that depends on spatial data. A number of generally applicable functions have been developed, see Table 2.
The most useful, census relevant, function is probably the equality zoning; in which regions are devised that are of near equal value in terms of a selected variable; for example, population, size, or numbers of economically active. This has some similarities with a cartogram except that here the aggregation process reduces the number of original zones. Equal value zoning is useful because it controls for spatial size variation and there are a number of applications for which this is useful, whereas the cartogram is purely a cartographic device.
Optimising a zoning system with respect to a correlation target is of interest mainly to demonstrate aggregation or modifiable areal unit effects. However, it may also have some value as the basis for spatial analysis via mapping zoning systems that match a particular correlation target. This is discussed further in the next section. The distance function option is a further development in this direction. The AZP procedures attempt to fit a distance decay function to the data with respect to a user selected central point. The zoning systems that match such a model may also have some intrinsic geographical value. The spatial autocorrelation function is of interest because it represents a measure of global map pattern. Zonings that for a specific variable match particular autocorrelation targets may sometimes be of interest. The space partitioning function is equivalent to a form of location-allocation model. The regions are designed to maximise internal weighted accessibility. The result is a highly efficient partitioning of space. Finally, the similarity based zoning provides an AZP version of a contiguity constrained classification or regionalisation of the data.
Other zone design aspects are also relevant. In particular, it is not unusual to impose barriers upon the aggregation process; for example, to preserve key linear geographic features or to retain higher level administrative boundaries in the re-engineered zoning system. This can be easily introduced via deletion of contiguity links. The hard part is identifying and deleting the relevant links; and clearly a GIS can help here; for example, buffering and polygon overlay functions can be used to add barriers to the contiguity information.
Once an approximately optimal zoning system is defined new coverage needs to be generated that can be used subsequently in other spatial data handling operations. It is clear then that to be a viable zone design system the procedures need to be embedded within a GIS as the various separate functions need to be integrated. Table 3 provides a summary of the major steps in this process. If zone design methods are to be packaged for more general use, then this complexity needs to be hidden behind suitable user friendly interfaces.
Two sets of AML programs have been written in order to make AZP an easy-to-use application in Arc/Info. One is called ZDTools which allows the user to run AZP from a command line; the other is called ZDMenu which provides the user with a menu-driven system that will help to explore the various functions relating to zone design.
Both approaches are based on standard Arc/Info practice. The AML based ZDTool usage is given in Table 4. The equivalent menu based (ZDMenu) is outlined in Table 5.
Figure 1 provides a screendump of this menu driven interface to ZDES, outlining some of the choices. The results described in section 4 are produced by this system. Both the AMLs and the menu driven ZDES's are available from the authors.
Census digital ed boundaries and census data for the 2,926 eds in Merseyside is used to illustrate the ZDES system. Initially attention is focused on the distribution of old aged persons (males aged 65 and over and females aged 64 and over) on the grounds that these data are interesting in a substantive sense and are also a reasonably "hard" data set to re-zone. The hardness results from the sparsity of the data; not all eds have old people in them (indeed 113 had none) and this will provide a good test of the various zone design methods. The zero's will result in a larger than usual number of no data changes; ie the zoning system changes but the data and the zone design objective function does not. Additionally, the separation of the Wirral from the rest of Merseyside by the river Mersey splits the 2,629 eds into two super-regions or contiguity islands. This is interesting not least because this might be expected to be a common feature with digital census boundaries for small areas; for example, due to physical features causing logical contiguity breaks in census ed geography. There is no easy solution to the problem other than to redefine what is meant by contiguity and then add "artificial" linkages to the data.
One immediate consequence of the two contiguity islands is that the initial random zoning system generator based on Openshaw (1977c) will no longer ensure that each subregion has an appropriate share of the initial M regions. The algorithm was modified to first scan the contiguity information to identify the number of internally connected islands within it; second to identify each "island's" allocation of the M regions according to its share of a relevant variable (ie population), and finally to generate random zoning systems within each island. This might be regarded as spatially stratified random zoning. Another solution to the same problem is to use seed points as 'cores' for the random zoning system. ZDES offers all three.
This problem might be regarded as a basic spatial representational issue since it concerns how many regions a given island or subregion has to represent it. It also emphasises the risks of applying global spatial analysis and spatial models to census data without stopping to think about its structure; for example, if you were fitting a spatial regression model would you have one or two?
Interest here focused on the re-zoning of the census eds to produce regions that contained about the same numbers of old people as a test of the relative efficiency and performance of the three AZP algorithms.
The objective function is
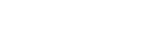 (5)
(5)
where
ij = 1 if zone i is in region j, else 0;
Pi is the number of old people in ed zone i; and
Tj is the target size for region j
Note that considerable compute time is saved by updating rather than recomputing equation (5) everytime any zone moves. This also makes the compute time needed to calculate the objective function invariant of N and M; a highly useful property whenever it can be done; although the total number of function evaluations depend on N and M.
Table 6 shows that generally the performance of the basic algorithm is good for small number of regions but starts to deteriorate once more than a 100 regions are involved. The basic tabu version is better but becomes less reliable for over 150 regions. The reactive tabu would be even better but is unaffordable even with these data because of very long compute times. The simulated annealing results are best throughout. However, the compute times in Table 7 provide a compelling reason why in a workstation environment the basic algorithm's poorer results might be acceptable in many practical applications. The disbenefit of attaining good rather than nearly optimal results may not always matter.
A potentially interesting use of the AZP algorithms is to provide a new approach to the map based analysis of census (and other spatial data). Consider for example the study of ethnic minorities on Merseyside at the ward scale; a level of aggregation commonly used in practice. Figure 2 shows the percentage of population belonging to an ethnic minority for the 119 census wards. The choropleth map is hard to interpret partly because of size variation in the wards with the result the map emphasises extreme results typically found in the smallest wards and is, therefore, mainly dominated by variations in ward size both in terms of physical size and population. Figure 3 presents the same variable but for a 119 zone approximately equal population aggregation of the 2926 census eds. The patterns are clearer but the visual impression is quite different. There are no longer such extremes of ethnicity (the maximum percentage is 4.97 compared with 27.7 in Figure 2). Moreover, the highest ethnic areas have moved northwards. Clearly these differences require further investigation but they illustrate how 'unsafe' spatial maps of census data can be. It is likely that a more even distributed variable would be much less affected. Figure 3 also illustrates another aspect of this form of zoning. Indeed, because the 119 zones are almost identical in size, raw counts could have been mapped directly because the denominators are virtually the same everywhere. Figure 4 presents a density surface for these zones to illustrate this point.
Equal population zoning is regarded as an extremely useful re-aggregation of census data for many purposes because:
(1) the areas are of nearly equal size thereby removing the confounding effects of size;
(2) the data precision for each new zone is the same so that differences in the mapped patterns reflects the variables being studied rather than either small number effects or sampling variability (more relevant for 10% census data); and
(3) the areas are size comparable, so they could more readily be ranked or subjected to other forms of spatial modelling.
The principal problem is that the results are only one of possibly many different but nearly equivalent equal population zonings. Furthermore, controlling for denominator size may not be sufficient. It might also be necessary to bias the results such that the regions are less heterogenous in terms of a number of other variables; for example, social class. Whether controlling for these effects is a zone design or a spatial modelling issue, is a matter for further investigation. The objective here is to provide the tools needed to support further research.
A final illustration of the usefulness of optimal zoning as a census analysis and visualisation tool is provided by looking at the correlation between unemployed and households without cars. At the census ed level, these two variables are highly correlated; r=0.99. The challenge now is to investigate the range of different map zoning systems than can yield very different results. Table 8 shows that very different correlation targets can be obtained. Note how the basic AZP algorithm works well when the problem is easier to handle; for instance when the ratio of N to M is large. As the number of regions increase so the simulated annealing starts to produce better results, albeit with a vast increase in compute times. Easy targets such as correlation of 0.0 for 50 regions took AZP 16 seconds. The harder target of -1.0 took the simulated annealing version 9,011 seconds. The targets of 1.0 were easily attained by the basic algorithm.
Fitting a linear model by changing simultaneously both the parameters and the aggregation provides an interesting opportunity to investigate whether or not the zoning systems themselves contain any useful geographic information about the variables under study. In this case, it is seemingly of considerable interest to investigate the nature of the zoning systems able to change a very strong positive correlation at the ed scale into a very strong negative association after aggregation into a much smaller number of regions.
Figures 5, 6 and 7 show the zoning systems that result, when the correlation targets of +1.0, 0.0, and -1.0 are specified. It is conjectured that the pattern of these zones contain useful insights about the relationship between scale, aggregation, and the variables of interest. The target of +1.0 is attained by having some very large and small zones. The target of 0.0 requires zones of almost equal size, with a high degree of compactness. The -1.0 target requires an extremely irregular set of zones. It would be interesting to explored further what happens as the numbers of output regions change and also to look at scatter plots of the data that the zoning systems create. Clearly ZDES marks the start rather than the end of the spatial analysis process.
It is noted that there are two opportunities for census zone design. The first is when the census agency makes decisions about the spatial framework used to report the census; the second is when the user considers what set of areal units best suit a particular analysis objective. GIS frees the need for census data to be reported for a fixed set of areas. There is no longer, in principle, any reason why census data for 2001 could not be reported for areal units, different from eds, but small enough and homogenous enough to be really useful spatial building blocks, whilst also being large enough to be confidentiality safe. Eds are really of only internal and administrative relevance to the census agency, indeed their widespread use in census analysis is a reflection of expediency. Even in an ideal world, census users would still want to re-engineer their zoning systems; but their task will have been eased by the provision of good initial building blocks much better than the census ed. Computers are now fast enough to routinely perform the second re-engineering and long before the next census is due, they will also be able to handle the initial zone design task too.
Meanwhile, with the 1991 Census, the onus of re-engineering census geography to at least reduce the problems, rests with the census analyst. At least some basic general purpose tools now exist to ease this task, the principal remaining difficulties concern the choice of suitable zone design functions best for particular purposes and the need to improve user awareness of the problems of studying spatially aggregated data.
Acknowledgement
The research reported here was funded by the ESRC Census Initiative, under award A507265011.
Aarts, E., Korst, T., 1989 Simulated annealing and Boltzmann machinesWiley, London
Amrhein, C., 1992, 'Searching for the elusive aggregation effects using age/sex specific migration data', The Operation Geographer 10, 32-38
Amrhein, C., Flowerdew, R., 1992, 'The effect of data aggregation on a Poisson regression model of Canadian migration', Environment and Planning A, 24, 1381-1391
Arbia, G., 1989, Spatial Configuration in Statistical Analysis of Regional and Economic related problems Kluwer, Dordrecht
Battiti, R., Tecchiolli, G., 1993, 'Training neural nets with the reactive tabu search' (unpublished MS)
Battiti, R., Tecchiolli, G., 1992, 'Parallel biased search for combinatorial optimization: genetic algorithms and TABU', Microprocessors and Microsystems 16 351-367
Battiti, R., Tecchiolli, R., 1994, 'The reactive tabu search', ORSA Journal on Computing (forthcoming)
Bland, J.A., Dawson, G.P., 1991 'Tabu search and design optimisation', Computer-Aided Design 23, 195-201
Carver, S., Charlton, M.E., Rao, L., 1994, 'GIS and the Census' in S. Openshaw (ed) Census Users Handbook Longmans, London
Denham, C., 1993, 'Census geography: an overview', in A. Dale and C. Marsh (eds) The 1991 Census User's Guide HMSO, London p52-69
Dudley, G., 1991, 'Scale, aggregation and the Modifiable Areal Unit Problem', The Operational Geographer 9, 28-32
Fotheringham, S., Wong, D., 1991, 'The modifiable areal unit problem in multivariate statistical analysis', Environment and Planning A 23, 1025-1044
Glover, F., 1977, 'Heuristics for integer programming using surrogate constraints', Decision Science 8, 156-166
Glover, F., 1986, 'Future paths for integer programming and links to artificial intelligence', Computers and Operations Research 13, 533-549
Glover, F, Laguna, 1992 'Tabu search', in (ed) Modern heuristic techniques for combinatorial problems Blackwell, London p?
Goodchild, M.F., 1979 'The aggregation problem in location allocation', Geographical Analysis 11, 240-255
Hertz, A., de Werra, D., 1987 'Using Tabu search techniques for graph colouring', Computing 39, 345-351
Kendall, M.G., Yule, G.U. 1950, An introduction to the theory of statistics Griffin, London
Kirkpatrick, S., Gelatt, C.D., Vecchi, M.P., (1983) 'Optimisation by simulated annealing' Science 220, 671-680
Metropolis, N., Rosenbluth, A.W., Rosenbluth, M.N., Teller, A.H., Teller, E., (1953), 'Equations for state calculations by fast computing machines', J. of Chemical Physics 21, 1087-1092
Monmomier, M., 1991, How to lie with maps University of Chicago Press, Chicago
Openshaw, S., 1977a, 'A geographical solution to scale and aggregation problems in region-building, partitioning, and spatial modelling', Trans. Inst of British Geographers New Series 2, 459-472
Openshaw, S., 1977b, 'Optimal zoning systems for spatial interaction models', Environment and Planning A 9, 169-184
Openshaw, S., 1977c, 'Algorithm3: a procedure to generate pseudo random aggregations of N zones into M zones where M is less than N', Environment and Planning A 9, 1423-1428
Openshaw, S., 1978a, 'An empirical study of some zone design criteria', Environment and Planning A 10, 781-794
Openshaw, S., 1978b, 'An optimal zoning approach to the study of spatially aggregated data', in I. Masser and P.J.B. Brown Spatial Representation and Spatial Interaction Martinus Nijhoff, Leiden 93-113
Openshaw, S., Taylor, P.J., 1979, 'A million or so correlation coefficients: three experiments on the modifiable areal unit problem', in N. Wrigley (ed) Statistical Applications in the Spatial Sciences Pion, London
Openshaw, S., Taylor, P.J., 1981 'The modifiable areal unit problem', in N. Wrigley and R.J. Bennett (ed) Quantitative Geography Routledge, London 60-70
Openshaw, S., 1984, The Modifiable Areal Unit Problem CATMOG 38, Geoabstracts, Norwich
Openshaw, S., 1988, 'Building an automated modelling system to explore a universe of spatial interaction models', Geographical Analysis, 20 31-46
Openshaw, S., 1989, 'Learning to live with errors in spatial databases' in M. Goodchild and S. Gopal (eds) The accuracy of spatial databases Taylor & Frances, London 263-276
Openshaw, S., Gillard, A., 1978, 'On the stability of a spatial classification of census enumeration district data', in P.W.J. Batey (ed) Theory and Method in Urban and Regional Analysis Pion, London 101-119
Press, W.H., Flannery, B.P., Teukolsky, S.A., Vetterling, W.T. 1986, Numerical Recipes Cambridge University Press, Cambridge
Tobler, W., Moellering, H., 1972, 'The analysis of scale variance', Geographical Analysis 4, 34-50
Tobler, W., 1989, 'Frame independent spatial analysis', in M. Goodchild, S. Gopal (eds) Accuracy of Spatial Databases, Taylor and Francis, London 115-122
Table 1 Illustrative numbers of candidate zoning systems that could be evaluated in parallel
No of regions original number of zones
M N = 2926
5 522
10 784
20 923
30 1,114
40 1,408
50 1,516
100 1,964
200 2,424
300 2,929
400 3,247
500 3,702
Note The exact numbers depend on the configuration of the starting regionalisation
Table 6 Results for equal zone size objective function zonings
No of regions Algorithm
required AZP* AZP-TABU AZP-SA
10 15.6 12.1 15.2
20 153.8 238.3 64.0
30 232.7 128.2 158.3
40 538.8 253.2 287.9
50 815.7 569.2 367.8
75 1061.4 986.1 585.4
100 2239.0 1491.8 922.6
150 3800.6 4839.8 156.7
200 6860.2 10693.9 1765.9
Note
* The AZP result is the best from starting with 10 different random zonings. The TABU and SA results are unaffected by the choice of initial random zoning system
Table 7 Compute times (seconds) for zone size objective function rezoning
No of regions Algorithm
AZP AZP-TABU AZP-SA
10 730 5169 19575
20 1182 3306 9763
30 1671 2915 10679
40 1880 12828 10156
50 1861 3877 9903
75 2010 5684 10493
100 2053 5169 12579
150 2434 12876 13887
200 2229 7875 131766
Note: Compute times are for Sun-Supersparc 10 model 40 workstation
Table 8 Correlation between unemployed and no cars on Merseyside
No of regions target Method:
correlation AZP AZP-SA
error error
10 -1 .0019 .0009
50 -1 .025 .0013
100 -1 .1745 .0030
200 -1 .1998 .0267
10 0 .0000 not needed
50 0 .0000 not needed
100 0 .0000 not needed
200 0 .0000 not needed
10 +1 .0520 .0114
50 +1 .0217 .0033
100 +1 .0066 .0016
200 +1 .0095 .0009
Table 2 Standard zone design functions
equal value zoning
correlation
distance function
autocorrelation
space partitioning
similarity