
 |
Return to GeoComputation 99 Index
David Kidner1, Phil Rallings2, Ian Fitzell3, Miqdad Al Nuaimi3 & Andrew Ware2
University of Glamorgan
1School of Computing
2Division of Mathematics & Computing
3School of Electronics
Pontypridd, Rhondda Cynon Taff
WALES, U.K. CF37 1DL
E-mail: dbkidner@glam.ac.uk
Radio communications planning has been a prominent application area of digital terrain modelling for the last 30 years. With increased de-regulation in the telecommunications sector and a growing number of network providers, the resulting variety and complexity of networks using the radio spectrum has made the task of the radio planning engineer more critical than ever (Ansary, 1999). In addition, the range of radio communication modelling scenarios (and associated variables), coupled with the higher resolution terrain and topographic data sets now available, make radio path and network planning a very computationally demanding process. This is particularly significant for determining broadcast coverages in the field-of-view. One solution is to parallelise the application. The need for specialised hardware is no longer an obstacle to producing parallel solutions, as recent advances in modern operating systems allied with PC networks are available in most organisations. The real problem is identifying the best strategy for assigning the workloads to machines, which minimises both the processor redundancy and communication overheads. This paper presents the issues for developing a distributed GIS for radio propagation modelling and presents a domain decomposition strategy that optimises performance over hilly terrain. The results are extremely encouraging, suggesting that speed-up performance can be increased by a factor of 19 or more using only 20 PCs. The strategy can also be extended to urban landscapes with the integration of 3-D data models for representing surface features such as buildings and vegetation.
The 1990s have witnessed a resurgence of digital terrain modelling in the GIS arena, particularly for applications within a planning context, such as environmental impact assessment, visibility analysis, and radiocommunications planning. As larger scale digital terrain models (DTMs) have become available, the higher resolution and improved accuracy have tempted more organisations to invest in GIS as a cost-efficient decision support tool. This is particularly evident in the radiocommunications field, which has vociferously lobbied for better terrain and topographic databases. For example, Edwards & Durkin (1969) were among the first to recommend a strategy for developing a regular grid digital elevation model (DEM) from contour maps, together with intervisibility and radio path loss algorithms; however, for such applications, inaccurate or misleading results can be counter-productive and expensive to remedy. Hence, radio planners are seeking to develop more accurate data models and algorithms to improve path loss predictions.
Path loss models describe the signal attenuation between the transmitter and receiver as a function of the propagation distance and other parameters related to the terrain profile and its surface features. Many of the problems of radio propagation are akin to the problems of intervisibility analysis, i.e., choice of data model (grids versus TINs); DTM scale or resolution; profile retrieval algorithm; incorporation of ground cover data; and verification of the predicted results. Although many users (and certainly most GIS) simplify the intervisibility problem by ignoring ground cover data, or clutter, this is no longer a valid option for accurate radiocommunications planning. Clutter can include buildings and other relevant properties including roof structures, building materials and heights; vegetation and shrubbery, including individual trees; and other 2-D surface features that have distinctive propagation properties, such as roads and water bodies.
With the current boom in the mobile cellular telephone sector, each company aims to provide the most complete network coverage, so the need to identify and plan for weak signal areas is crucial. As the power of computing has increased, then the viability of producing accurate large scale predictions of a transmitter service area, using well developed radio communications tools and algorithms, has become a reality. The results that have been obtained using this approach have proved to be of some merit, but the levels of accuracy are sometimes below the requirements of the end user. Furthermore, some prominent members of the radio communications community have suggested that unless this situation improves, then a return to manual methods of analysis could be a real alternative. For example, radio attenuation is evaluated from statistical propagation models in which no specific terrain data are considered, and channel parameters are modelled as stochastic variables.
In radio communications, planners are essentially concerned with developing GIS for determining the suitability of proposed point-to-point communication links (Figure 1) and also the area coverage of a proposed transmitter (Figure 2). The former is concerned with providing channels of communications between sites, thus requiring an accurate estimate of the terrain cross-section, together with any obstructions or clutter, which may cause interference. Area or broadcast coverages extend this problem into a given geographical region, such that areas of good communication (above minimum signal strength for the receivers and acceptable levels of interference) can be identified, together with shadows, where reception may be unsatisfactory. These problems can again be compared with the more traditional GIS intervisibility functions of calculating line-of-sight profiles and viewsheds.
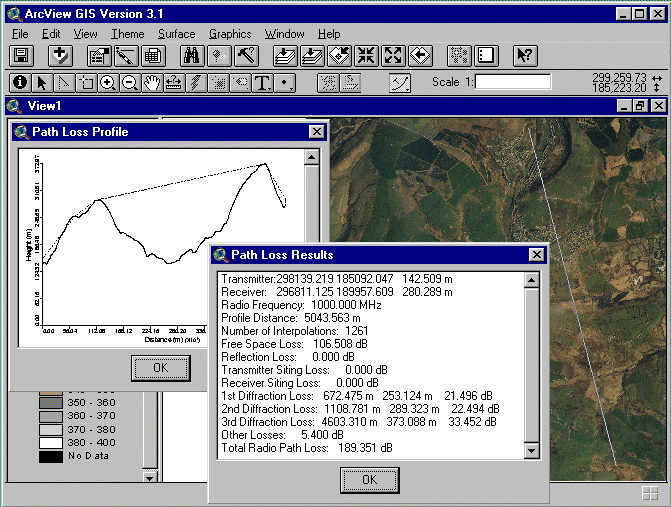
Figure 1 - Point-to-Point Radio Path Loss Propagation Algorithm
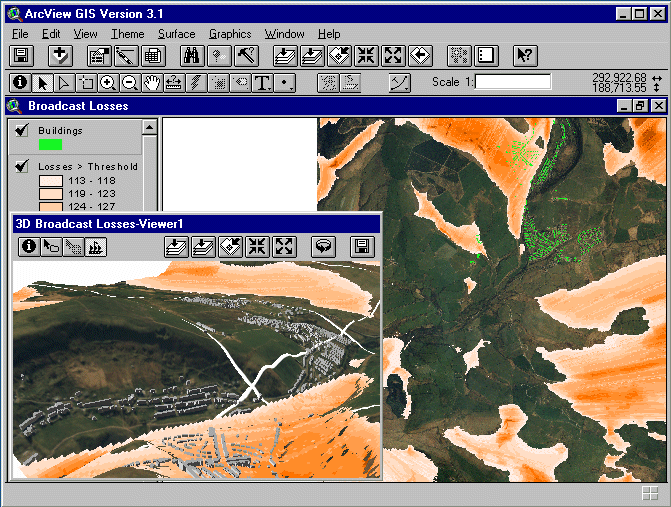
Figure 2 - Radio Broadcast Area Coverage (Shaded Regions Indicate Shadows or Signal Losses Above the User-specified Threshold)
For planning purposes, a GIS is very good for exploring what if scenarios, or more specifically in our case, for identifying potential sites for a transmitter (as in Figure 2); however, while the GIS can report back a multitude of statistics such as the number of receiver locations above or below the minimum signal strength; the number of buildings within the shadow regions; the demographic profiles of people living within the broadcast coverage; or produce maps and other visualisations of these results; it is rather limited as a true spatial decision support system. In particular, rather than test the suitability of specific transmitter locations, radio planners would prefer an optimal solution, such as the transmitter location that maximises geographic coverage, or maximises the number of homes within an acceptable signal strength tolerance. The practicality of meeting this goal is dependent upon implementing an efficient strategy for processing hundreds or thousands of individual area coverage calculations for possible transmitter locations. Each calculation may require individual point-to-point propagation calculations to hundreds of thousands or millions of locations (i.e., DEM vertices). Each point-to-point calculation may in turn require the interpolation of thousands of terrain profile elevations from the DEM, that could use a more accurate, but ultimately more time consuming algorithm than the traditional bilinear function (Kidner et al., 1999). Along each step of the profile a topographic database of surface features also may need to be queried. It soon becomes apparent that the problem is non-trivial, and perhaps unrealistic. In trials on a number of different data sets, some of these searches for optimal transmitter locations required up to 2 weeks of continuous processing on a Pentium II. Quicker solutions are possible, but at a cost of reducing the workloads, accuracy, hence confidence in the results.
This paper outlines our strategy for parallelising the problem of determining optimal transmitter locations. The following sections consider the basics of radio propagation models, the integration of topographic models with the DEM, and the options for parallelising these workloads.
The essence of radio communications planning is the prediction of the expected path loss over a link between a transmitter and receiver to determine suitable sites. This paper will not address the processes of radio propagation in any detail, nor the specific algorithms required to estimate the different types of attenuation losses, but instead will introduce the basic concepts to give the reader an understanding of the level of computation required for accurate predictions. This understanding will hopefully lead to some approaches for parallelising the problem.
The benchmark against which we measure the loss in a transmission link is the loss that would be expected in free space, or in other words, the loss that would occur in a region that is free of all objects that might absorb or reflect radio energy. Line-of-sight (LOS) for radio links is similar to the definition of LOS for visibility analysis, i.e. two points are said to be LOS if they are intervisible; however, in some cases, links may have a LOS path even though they are not intervisible. This is because the radio horizon extends beyond the optical horizon. Radio waves follow slightly curved paths in the atmosphere, but if there is a direct path between the antennas that do not pass through any obstacles, there is still radio LOS.
A LOS radio link does not necessarily mean that the radio path loss will be equal to the free space case. Differences may arise due to:
When a path is not LOS, it becomes even more difficult to predict how well signals will propagate over it. Unfortunately, non-LOS situations are sometimes unavoidable, particularly in urban areas. The simplest case is to consider the diffraction loss at this obstacle by thinking of it as a knife-edge. There are a number of algorithms available to planners that model these diffraction losses. More often, planners are faced with considering multiple obstacles such as rooftops, many of which do not resemble knife edges. Radio paths will also often pass through objects such as trees and wood-frame buildings that are semi-transparent at radio frequencies. Many models have been developed to try and predict path losses in these more complex cases. Different surface features will exhibit different propagation properties, all of which will need to be taken into account for accuracy.
Radio propagation between two unobstructed points is now well-understood and easily calculated. For these paths, differences between mathematical calculations and actual field measurements are quite small; however, when considering obstructed radio paths, which is quite common for urban radio planning, radio coverage is difficult to calculate. In fact, under these circumstances, coverage cannot be accurately determined, only predicted. Kidner (1991) considers the problems of estimating radio path loss with respect to different types of digital terrain models with different accuracies. But as geographical data capture becomes more precise at higher resolutions, it is hoped that these predictions can become more accurate.
Figure 3 outlines the generalised steps involved in determining the optimal location for a new transmitter. These steps can vary, depending on the specific details of the radio planner's query, for example, atmospheric losses might only be calculated at frequencies well into the microwave region. In addition, some aspects of this algorithm can be complex problems in their own right, such as the DEM profile retrieval algorithm, the calculation of diffraction losses, and the calculation of reflection losses; however, the generalised algorithm presented in Figure 3 demonstrates the methodical approach to solving the problem, and identifies some of the specific tasks that could be parallelised.
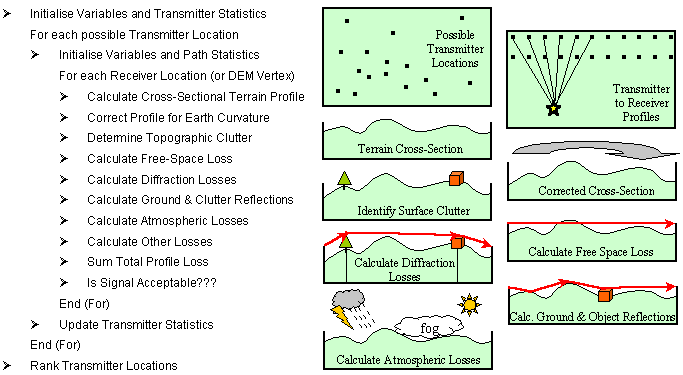
Figure 3 - Generalised Algorithm for Determining an Optimal Transmitter Location
To date, many of the attempts to computerise radio path loss prediction have focused on small- to medium-scale analysis. At these scales, geographic features are generally captured or represented as clutter categories from maps or satellite imagery (Hurcom, 1996), if at all. Typical examples of categories could include dense urban, suburban, vegetation and water features; however, the accuracy of these models gives some cause for concern. Typically, algorithms may attempt to model the general propagation properties of these features, possibly from look-up tables. Ideally, the features need to be encapsulated accurately within 3-D data structures that can be easily integrated with the underlying DEM. Dorey et al. (1999) present an overview of some of these approaches, particularly with respect to DEMs and triangulated irregular networks (TINs). The benefits of doing so are clearly evident with respect to increased accuracy. As a comparison, intervisibility analysis at a DEM source scale of 1:10,000 in a hilly, partly-developed landscape was shown to be correct less than 40% of the time (Dorey, et al., 1999). When topographic features are integrated with the DEM, the accuracy almost doubles.
Existing commercial data sets fail to supply all of the information that a radio planner would require for propagation modelling at large scales. As a result, new initiatives have been proposed to generate data specifically for this application area, together with data models to support their more widespread use (DERA, 1996). For example, data structures have been proposed to handle multiple levels of 3-D buildings with a variety of extrusions, sloping walls, walkways; each with their own roof structures defined as ridges with heights; together with details of the building materials (hence, propagation or reflection properties); however, the complexity of these data models, and the tendency to support data transfer with the use of limited data structures (such as those found in DXF or VRML), do not encourage their widespread integration with GIS, particularly commercial systems. Instead, users require the flexibility of their own data structures and software to make the most of this data for applications such as radio path planning.
The last couple of years though have seen a revolution in spatial data acquisition techniques. Soft-copy photogrammetry and Light Detection And Ranging (LiDAR) (see Figure 4) have now become more accessible to a wider market with falling data capture costs, but at increasing accuracy and precision. Such sources of data will open up many new and different types of GIS analysis for a much wider audience in the future; however, it is essential that we have the software tools in place now to support these developments. For example, radio path planning was traditionally applied to the rural landscape with GIS, but now urban applications are more widespread. The capability to handle these extensive new 3-D data sets and integrate them with existing DEMs or TINs also requires much greater processing power, thus giving wider credence to the need for parallel algorithms.

Figure 4 - LiDAR 2km x 2km DEM of Suburban District of Cardiff Sampled at 2-m Resolution
Parallel processing has been proposed as a solution to computationally demanding problems for many years, but despite extensive research its general application still appears to be a distant prospect (Downton & Crookes, 1998). In the GIS domain, there is a reluctance to take this technology forward beyond the realms of academia. While demonstrating the benefits of parallel processing, Gittings et al. (1993) also state that considerable effort may sometimes be required to design appropriate algorithms that can exploit parallel architectures. Much of the early research on parallel GIS algorithms focused on using fine grain architectures or Transputer networks. In most instances, a detailed understanding of the hardware configuration was essential, while many of the algorithms were programmed in specialised languages, such as OCCAM. Coupled with the cost of the specialised hardware, users were reluctant to invest the time, energy, and money into what was seen as something of a luxury. Today, the increasing availability of computer networks in the workplace, combined with recent advances in modern PC operating systems, means that many organisations already have an existing multipurpose parallel processing resource that could be used to carry out such tasks. Operating systems that are able to support these environments include Windows NT, OS/2, LINUX, Solaris, and to a limited extent, Windows 95 (Rallings et al., 1999). Furthermore, today's parallel user requires flexible, portable software, rather than having to re-write code. Distributed (cluster) computing allows for the original source code (e.g. in C) to be re-used on each computer with little or no modification.
General-purpose network hardware is not designed for parallel processing systems, especially when masses of data have to be passed between systems. Latency is very high and bandwidth is relatively low compared to specialised parallel processing environments; however, recent developments in network technology make it possible for workstations to have a higher shared bandwidth or a dedicated bandwidth. For example, the cluster shares a 100 mega-bit per second (mbs) bandwidth or each machine has its own 10 mbs bandwidth. Message passing and communication is the main overhead when using a parallel cluster and is an issue that must be addressed when implemented into GIS applications (Rallings et al., 1999). The problem becomes more complex if a heterogeneous network of different machine architectures is used, as some message encoding system must be incorporated for effective communication. Rallings et al. (1999) provide an overview of readily available software for assisting the implementation of distributed systems, including PVM, Express, MPI, and LINDA.
One of the main drawbacks to the wider use of parallel processing is the difficulty of detecting the inherent parallelism in problems. For example, consider an everyday GIS operation such as polygon overlay (Harding et al., 1998). Different parts of this algorithm are ripe for parallelism, such as the search for possible intersecting polygons, the intersection check for each pair of line segments, and the linking together of the new polygon components. Naturally, this leads us to consider splitting the algorithm into a number of sub-processes and performing each on different processors concurrently. This approach is termed algorithmic or function parallelism (Healey & Desa, 1989; East, 1995). Figure 3 illustrated each of the separate processes that need to be performed for determining our optimal transmitter location. On first impressions, the algorithm seems to be well suited for function parallelism; however, other factors need to be considered, such as the workload of each processor and the communication overheads. The alternative approach is to use the serial algorithm on each processor, but to partition the data set or domain over which each processor will perform the necessary computations. This partitioning is known as geometric or domain parallelism. With respect to our problem, one approach might be to segment the DEM (or receiver locations) into equal-sized blocks. This requires efficient communication methods for reading data from disk, distribution of the data amongst the processors, gathering the resultant data from the processors, and writing data to disk (Mineter, 1998). The partitioning can be achieved either statically (pre-assigned DEM segmentation) or dynamically, in which the domain segments are assigned as processors become available. This method can be taken further by considering another dynamic approach to domain parallelism in which the workloads per processor are minimised (e.g., one area coverage calculation per processor at a time), with a master processor distributing these tasks to processors as they become available, and collating the results from each in turn. This general approach is known as event parallelism or farming (Healey & Desa, 1989; East, 1995); however, as the farming is dependent upon the time taken for a processor to complete its workload, there is an implicit relationship with the topography of the transmitter location and the size of the area assigned to it for calculating broadcast coverage. Hence, the approach can be considered a hybrid of event and domain parallelism. Dynamic farming is best suited when workloads may be uneven, either because of the nature of the topography, or different machine specifications on the network.
To evaluate the practicalities of parallelising our serial radio path loss algorithm, a number of data sets were chosen for analysis. In each case, the aim was to identify the optimal location for a new transmitter. Each data set had different degrees of topographic features, ranging from a built-up city to a rural landscape. In the first instance, we have considered these features to be an extension of the terrain with respect to diffraction and reflection properties. For example, consider the DEM for Gilfach Goch in South Wales (Figure 5), covering a 5km by 5km region sampled at a resolution of 10 m. Possible transmitter locations were found on the basis of being a local maximum, using a simple search kernel. This identified 520 possible locations (Figure 5). This example requires more than 130 million transmitter-to-receiver radio path loss calculations to determine the optimal location.
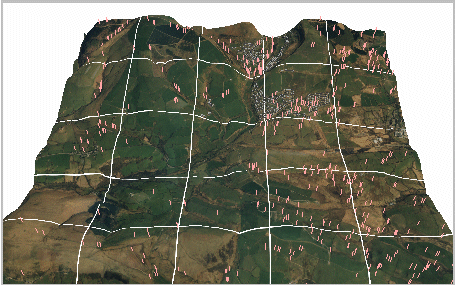
Figure 5 - The 520 Possible Transmitter Locations Used for Determining the Optimal Area Broadcast Position within a 5km x 5km O.S. 1:10,000 Scale DEM in South Wales
A number of parallel strategies as outlined above in Section 4 were examined for optimising the problem. In all cases these considered a static or dynamic partitioning of the domain (i.e., the DEM). Static algorithms were largely unsuccessful, as it is virtually impossible to ensure a completely load-balanced system, i.e., equal workloads for each processor. In particular, static algorithms were notably poorer when the DEM was partitioned into specific regions, such as blocks or rectangles. The nature of the terrain dictates the amount of processing in certain regions. For the transmitters in Figure 5, the time taken to calculate the broadcast coverage varied by up to 200% of the quickest transmitter time. As such, static algorithms will only become optimal if the terrain characteristics can be recognised in advance of the partitioning. Dynamic partitioning produced more efficient performances suggesting well-balanced distributed systems; however, tests showed that for this problem, optimal performance was achieved by assigning a workload of one complete broadcast coverage per processor, i.e., without segmenting the DEM itself. This requires that the complete DEM be available to each machine; thus, there is an initial overhead in communicating this DEM to all machines on the network at the outset. The communication overheads can be noticeable if each processor returns a complete broadcast coverage array of the same dimensions of the DEM; however, this problem was overcome by analysing the results locally on each machine to determine its suitability. Once a machine finishes its broadcast calculation, the master processor assigns another transmitter location for processing to that machine. The amount of message and variable passing is relatively low, which suits a dynamic farming approach. There was no evidence to suggest that as the number of machines on the network increased (up to twenty PIIs in these experiments), that the communication overhead becomes unmanageable. The results for this dynamic farming approach are presented below in Table 1.
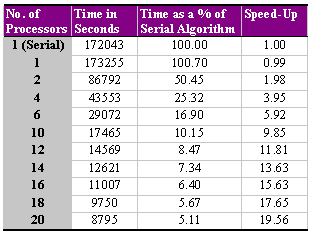
Table 1 - The Results for the Parallel Radio Broadcast Algorithm Applied to 20 Pentium IIs for the South Wales Data Set of Figure 5
The workload consists of performing more than 130 million transmitter to receiver path loss calculations, which, on a Pentium II running at 233 MHz, took 47 hours and 47 minutes. The equivalent workload using a parallel algorithm on the same machine required about 20 minutes longer. This was due to the configuration of the communication protocols and message passing, which needed to be in place. In effect, the machine in this instance is acting as both master (in controlling the farming of work) and slave (in performing each broadcast coverage calculation). When more than one machine is used, the speed-up time is almost linear. For this problem, the communication overheads are negligible; however, if we passed back the complete broadcast coverage, then the speed-up performance started to tail-off from this linear relationship, particularly as more processors were added. In effect, the network can become swamped with data to such an extent that if more processors are added the problem becomes untenable, but by analysing the performance of the results locally and returning just a summary of the results, communication overheads do not become a problem.
The practicality of parallelising many GIS operations is now within the reach of many users, such as corporate industry, academia, local and national government, environmental agencies, and in this case, broadcasters, without the need for any further investment. The key to unlocking this opportunity is to demonstrate how existing resources (i.e., networked computers) can be used for popular but processor-intensive tasks.
This paper demonstrates the simplicity of our approach for the computationally demanding problem of optimising radio path planning for locating new transmitter sites. By divising a workload assignment algorithm that minimises the communication overheads between machines, an almost linear speed-up in performance can be achieved, i.e., using 20 PCs, the problem can be evaluated more than 19.56 times faster.
Many GIS algorithms are conceptually very simple; however, more often than not, it is the sheer magnitude of spatial data that requires processing that generates the bottleneck in GIS. But for application areas such as radio path planning and visibility analysis, the problem will get worse as users demand higher resolution DEMs and integrated, complex 3-D topographic data. In such instances, parallel processing can offer viable solutions. The problem is no longer one of unfamiliar parallel architectures and specialised software, but one of identifying the best strategy for partitioning the problem workspace and minimising the communication overheads. It still remains to be seen whether the GIS community will adopt parallel computing, but the technology and hardware are now within our reach.
Ansary, P., 1999. GIS - A Major Aid to Telecommunications Planning, http://www.lsl.co.uk/papers/telecomgis.htm
D.E.R.A., et al., 1996. Proposed Format for 3-D Geographical Datasets, Version 2.1 of the Report for the Technical Working Party on Mobile and Terrestrial Propagation, Defence & Evaluation Research Agency, Malvern, England.
Dorey, M., A. Sparkes, D. Kidner, C. Jones and M. Ware, 1999. "Terrain Modelling Enhancement for Intervisibility Analysis," in Chapter 14 of Innovations in GIS 6, Ed: B. Gittings, London: Taylor & Francis.
Downton, A. and D. Crookes, 1998. "Parallel Architectures for Image Processing," Electronics & Communication Engineering Journal, Vol. 10, No. 3, pp. 139-151.
East, I., 1995. Parallel Processing with Communicating Process Architecture, London: UCL Press.
Edwards, R. and J. Durkin, 1969. "Computer Prediction of Service Areas for V.H.F. Mobile Radio Networks," Proceedings of the IEE, Vol. 116, No.9, pp. 1,493-1,500.
Gittings, B.M., T.M. Sloan, R.G. Healey, S. Dowers and T.C. Waugh, 1993. "Meeting Expectations: A Review of GIS Performance Issues," in Geographical Information Handling - Research and Applications, (Ed: P.M. Mather), Chichester: John Wiley & Sons, pp. 33-45.
Harding, T.J., R.G. Healey, S. Hopkins and S. Dowers, 1998. "Vector Polygon Overlay," in Chapter 13 of Parallel Processing Algorithms for GIS, (Eds: R.G. Healey et al.), London: Taylor & Francis, pp. 265-288.
Healey, R.G. and G.B. Desa, 1989. "Transputer-Based Parallel Processing for GIS Analysis," Proc. of Auto-Carto 9, ACSM/ASPRS, pp. 90-99.
Hurcom, S., 1996. "Radio Propagation Modelling," Mapping Awareness, October, pp. 22-25.
Kidner, D.B., 1991. Digital Terrain Models for Radio Path Loss Calculations, Ph.D. Thesis, The Polytechnic of Wales, p. 269.
Kidner, D., M. Dorey and D. Smith, 1999. "What's the Point? Interpolation and Extrapolation With a Regular Grid DEM," Proc. of GeoComputation '99, VA (These proceedings).
Mineter, M.J., 1998. "Partitioning Raster Data," in Chapter 10 of Parallel Processing Algorithms for GIS, (Eds: R.G. Healey et al.), London: Taylor & Francis, pp. 215-230.
Rallings, P., D. Kidner and A. Ware, 1999. "Distributed Viewshed Analysis for Planning Applications," in Chapter 15 of Innovations in GIS 6, Ed: B. Gittings, London: Taylor & Francis.