
 |
Return to GeoComputation 99 Index
James A. Griffiths & Andrew J.C. Collison
Geography Department, King's College London, London WC2R 2LS, United Kingdom
E-mail: jim.griffiths@kcl.ac.uk
Steven Wade
WS Atkins Water, Woodcote Grove, Ashley Road, Epsom, KT18 5BW, United Kingdom
This paper describes a simple GIS-based slope-hydrology model, and examines its potential for use in estimation of future landslide activity with respect to climate change. The model was calibrated for humid-temperate (U.K.), and sub-humid (SE Spain) environments, and was found to simulate current water table fluctuation to a reasonable standard using just rainfall and temperature data. The implications of predictions produced using longer term downscaled GCM data are more debatable. If the sensitivity of the model to the natural variability of the input data is high for example, the model may not be able to distinguish more subtle longer-term changes in landslide activity. By comparison of model prediction for past climate data with that predicted for the future, an insight into how landslides might respond to climate change can be obtained. It is concluded that more useful prediction might be obtained by determining landslide sensitivity to the changing variability of the climate. Identifying the threshold conditions needed to cause instability might do this.
This study builds on work developed through the TESLEC (EC EV5V-CT94-0454), and NEWTECH (EC ENV4-CT96-0248) programs, which in addition to improving landslide management techniques, aim to increase the understanding of landslide probability with respect to changes in climate (Brunsden et al., 1996; Dikau et al., 1996; Dehn & Buma, 1996; Wade, Collison & Dehn, 1997; Van Asch and Buma, 1997). The latter program especially concentrated on the design of hydrological models that could be used to increase landslide prediction capability to more acceptable standards. A relatively simple 1-D model from this programme forms the basis of the distributed model described in this paper. The model was originally designed for shallow translational landslides and tested within humid-temperate and sub-humid environments.
Modelling landslide hydrology is not a new phenomenon and much work has already been done to simulate the internal dynamics of such landscapes. Physically-based models, especially, have become increasingly popular in recent years. The 1-D soil water - slope stability finite difference model of Anderson and Howes (1985), for example, has led to the development of a series of studies determining slope stability relative to climate, vegetation and pedogenisis of shallow translational landslides (Brooks and Richards, 1993); (Brooks, Anderson and Collison, 1995); (Collison and Anderson, 1996). Similarly, shorter-term pore pressure variation at the shear surface has been successfully simulated using both pressure diffusion models (Haneburg, 1991; Reid, 1994), and finite element schemes (Ng and Shi, 1998).
Three dimensional simulation of landslide hydrology has so far tended to be less prevalent due to the large amounts of input data required and longer computation times involved. Montgomery and Dietrich (1994), solved this problem to a certain extent by keeping the number of input parameters to a minimum, and by using a topographic wetness index to identify which areas within a catchment were most likely to become unstable first. In assuming steady state rainfall, however, the model is unable to predict temporal response of landslides to varying rainfall patterns. A more complex model by Dietrich et al., (1995), considered the additional effects of spatially varying soil and vegetation parameters. Though the model gave a greater insight into the controls of slope stability, its practical application was very much dependent on the availability of accurate and reliable calibration data.
The model described in this paper attempts to simulate moisture redistribution within the soil through a 'distributed tank-model' approach. Though not strictly physically-based, processes of evapotranspiration; infiltration; and throughflow can be represented using the dynamic modelling capability of the PCRaster GIS (van Deurson, 1995; Wesseling et al., 1996). The model is developed from a three layered, 1-D version that was used to estimate mean water table depth in response to long-term rainfall and temperature variation (Wade, Collison & Dehn, 1998). Similar to the approach of Montgomery and Dietrich (1994), described above, predictions from the 1-D model were initially determined for a given catchment using a function of the topographic index (Bevan and Kirkby, 1979). Although producing acceptable results, the model was unable to reproduce the spatial variation of groundwater that would result from throughflow and other inter-cell moisture movement. Predicted groundwater hydrographs for example, were of different relative magnitude but exhibited the same shape and response to rainfall. The model also was found to be unsuitable for use in drier environments of higher negative pore water pressure (such semi-arid parts of Spain), due to assumptions made within the topographic index.
In order to simulate the hydraulic response of a landslide over relatively long timescales, it was necessary to represent the physical nature of component hydrological processes in a relatively simple manner. The vertical soil profile is represented by just three layers: root zone, colluvium, and underlying impermeable layer; and a suitably scaled digital elevation model (DEM) is used to apportion the landslide laterally. For each cell then, processes of infiltration, unsaturated and saturated flow, and throughflow, are represented using a simple 'non-linear tank model' approach (Suawara, 1995). Gravity driven vertical moisture movement is simulated at a rate limited by soil conductivity and the capacity of the underlying layer to receive moisture. Horizontal movement is modelled in the direction of neighbouring cell of lowest moisture content, and at a rate determined by a derivative of Darcy’s Law. For each timestep, moisture movement is therefore modelled vertically between layers for each cell; and then horizontally, between cells of the same layer.
Definition of the soil profile is limited to three distinct layers in order to reduce computing time and simplify calibration procedure (though theoretically this could be increased for soils of greater heterogeneity). As illustrated in Figure 1, the total amount of water in each layer is calculated with respect to rainfall and evapotranspiration using the following simple water balance equations:
|
Layer 1: Wt+1 = Wt + {R(1- t)} - [EVTa(1-rc)] - D1 (1) |
|
Wt = initial water content, (mm) Wt+1 = water content after time t, (mm) R = net rainfall, (mm) t = bypass coefficient EVTa = actual ET, (mm) rc = root coefficient D1 = drainage from layer 1, (mm) D2 = drainage from layer 2, (mm) D3 = deep percolation, (mm) |
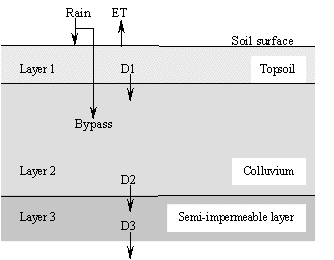
Figure 1: Schematic illustration of 1-D water balance model.
The model assumes infiltration is always greater than rainfall intensity due to the presence of biopores and fissures within the topsoil, though runoff will occur when the top layer is saturated. Drainage from a layer is assumed to occur to its field capacity but is limited by the capacity of the underlying layer to receive drainage. The rate of transfer of moisture from one layer to another is regulated by soil conductivity as defined by van Genuchten (1980). Total vertical percolation, saturation excess, and water content at the end of each time-step, will depend on one of four possible conditions:
i. No drainage from cell - amount of incoming water is insufficient to fill the cell micropores.
ii. Drainage from cell to field capacity - available water fills micropores, but is less than field capacity and potential to drain.
iii. Unconditional drainage - available water sufficient to maintain field capacity and maximum drainage, but cell not saturated.
iv. Unconditional drainage / saturation limited inflow - cell is saturated.
In addition, a certain amount of rainfall may enter directly into the second layer through tension and desiccation cracks. This phenomena is modelled as a logarithmic function of rainfall intensity, and is represented with the use of a bypass coefficient, as described by (Coles & Trudgill, 1985). Determined from empirical data, the bypass coefficient ranges from 0 (at a rainfall intensity where no macro-pore flow occurs between the top 2 layers), to a theoretical maximum value (<1), (at maximum expected rainfall intensity).
After calculation of vertical water flow, water content, equivalent water height, and pore-water pressure, gradient is determined for each cell within each of the three layers. To calculate the saturated horizontal flow component between cells, it is then assumed that vertical conductivity is effectively infinite and that flow is driven by the slope of the water table. A finite difference form of Darcy's Law, which describes the shape of the water table during steady flow towards a drain (Figure 2), was found to provide a good approximation of water movement downslope:
|
Qlat = [(Kn + Kn+1)/2][Zd - (Tn +Tn+1)/2](Tn+1 - Tn)/(Dx) (4) |
|
Qlat = horizontal flow, (mm2) Zd = height of soil layer, (mm) T = depth to water table, (mm) K = horizontal conductivity, (mm/day) x = horizontal distance, (mm) |
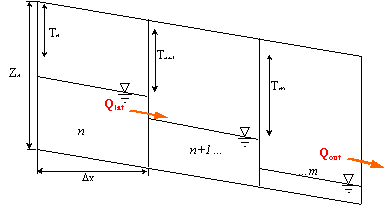
Figure 2: Slope profile divided into vertical strips (n to m), (after Scotter et al., 1990).
Flow is determined by the direction of neighbouring cells with lowest equivalent water depth, relative to a common datum. The procedure used to determine the extent of lateral flow in each timestep (see also Figure 3), may be summarized by the following steps:
i. Equivalent water height is determined for each cell within layer.
ii. Hydraulic gradient between adjacent cells of the same layer is calculated.
iii. Drainage direction between cells calculated for each soil layer.
iv. Downslope moisture deficit for each cell is calculated.
v. Water available for lateral flow from each cell is calculated.
vi. Lateral flow between cells, is determined as function of available moisture and moisture deficit of downstream cell.
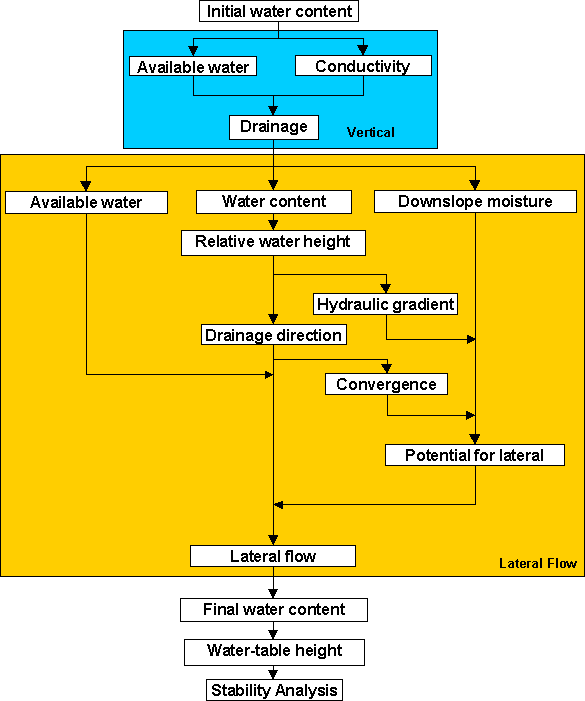
Figure 3: Schematic of PCRaster distributed water-balance model.
At the end of each timestep, the equivalent depth of water in each cell may be found. The method used assumes a linear and non-hysteretic soil water characteristic curve between soil matric potentials of 0 and -5 kPa (field capacity); and also that hydraulic equilibrium exists within each cell; hence, we may say,
|
T = [2(W0-W)/s]1/a (5) |
||
|
T = depth of water table in layer corresponding to equivalent water content W, (mm) W0 = capacity of layer (porosity x depth), (mm) W = water content, (mm) s = the slope of the soil moisture characteristic between saturation and field capacity a = empirically determined constant |
Cumulative water table height, for conditions of upper and lower layer saturation also can be calculated in order to ascertain total pore water pressure at the shear surface. At present no consideration is made of upward moisture movement within the model, however vegetation rooting depths may extract moisture from the second layer; hence, alleviating conditions of negative hydraulic gradient where capillary would become more significant.
In order to model ground water variation for monitored test sites, it was necessary to first account for soil, vegetation and topographic variability. Digital elevation models (DEMs), were obtained through a combination of aerial photography, map digitisation and ground survey. Practical limitations in reproduction of soil variability are imposed by the large amount of redistribution and reworking that occurs within relict or prone landslides. The advantage of using the GIS-based analysis package PCRaster, is that the sensitivity of the model to different vegetation or soil parameter distribution may be investigated. Distribution of soil porosity and saturated conductivity, for example, may be determined from interpolation of sampled data, thus reflecting more accurately the drainage characteristics of the slope as a whole.
At the Roughs test site in Kent, (U.K.), despite findings that indicate three distinct populations of soil and colluvium properties that reflect the underlying lythology of the area (Brunsden et al., 1996; Bromhead, 1997), field investigation by the authors found no significant spatial pattern to distributions of geotechnical properties, with the full range of variability being found at the scale within which the designed model was due to operate (10m2). Average values of residual shear strength (33.8 ± 9° [n=20]), porosity (0.45 ± 0.04m3/m3 [n=26]), and other hydrological parameters were used uniformly across the slope. Confirmation of the validity of these parameters was achieved using back-analysis for past events where the water table height was known. DEMs for the site were obtained through map digitisation and areal photography at resolutions of 10m and 5m respectively; ordinary kriging interpolation was used for both circumstances.
At the monitored site in Planes, (S.E. Spain), DEMs have been obtained at 5m and 10m resolution from University of Utrecht. Using the exact interpolation method of triangular irregular networks (TIN), allowed areas of greater topographic contrast (see Fig.4), to be better represented by a more intense sampling strategy (van Beek, 1998a). Parameter interpolation employed ordinary kriging or inverse distance depending on the variability and frequency of samples obtained (and qualitative assessment of produced semi-variograms). Mean porosity of the top layer of regolith-based soil was taken as 0.51 ± 0.05m3/m3, ranging from 0.42 to 0.65. Angle of internal friction is taken to be 34.8 ± 0.9°; for purposes of model analysis, effects of suction induced increase in shear strength is assumed negligible at low suction (van Beek, 1998b).
In order to reduce the amount of data required to run the model, evapotranspiration is calculated using a temperature dependent empirical relationship. Regression models were obtained for different vegetation types using meteorological data from the field sites and the Penman Monteith method. By using the same ET model for all types of vegetation, it is hoped that the driving parameters of vegetation may be reflected, and not merely the manner in which models treat meteorological variables (it is accepted that the ET model used might normally be considered as less ideal for some types of vegetation). Similarly, in using this method we are assuming that other meteorological variables (such as solar radiation, humidity, wind speed), will co-vary with temperature to a similar extent under climate change as they do under normal daily or seasonal variation. It may be suggested that only if this assumption is correct is it possible to make reliable temperature-based predictions of the effects of climate change through changing temperature only.
By using the regression model in some ways saves having to consider the more complex dynamics of other meteorological variables varying with climate change. Sensitivity analysis of the Penman-Monteith calculation, for example, suggests that relative humidity is the next most important meteorological parameter after temperature, followed by solar radiation and wind speed (McKenny & Rosenburg, 1993). Though the relative importance of these factors may change under different climatic zones and between seasons, Bevan (1979), suggests that within the same humid temperate environments at least, the extent of such variation will be secondary to change in aerodynamic and canopy resistance parameters. Response of ET to increased stomatal resistance and LAI such as might result from increasing C02 concentrations, were found to be of similar magnitude opposite in effect.
In modelling the effect of ET, it is extracted from the top two soil levels to an extent that is dependent on the root depth of the vegetation. Actual evapotranspiration (EVTa) is determined as a function of the soil's Available Water Capacity (AWC) and Soil Moisture Deficit:(SMD):
EVTa = EVTp.(1-SMD/AW) when SMD < AW (6)
EVTa = 0 when SMD AW (7)

Figure 4: DEM of monitored catchment and surrounding area in Planes, SE Spain, showing variation of the function log10 (Factor of Safety), for conditions of non-varying soil or vegetation parameters. Areas of potential instability for when soil is saturated to half its depth, are indicated by pixels of negative value. (For greater detail study of the same site see van Beek (1997)).
In the first instance, the suitability of the 3-D model was considered for the Roughs test site under present day conditions. Timeseries output of predicted local water table heights was determined for sampled cells within the DEM, and then compared with observations made in the field. Model parameters were calibrated and validated over a number of rainfall events between March 1996 and 1998, using both on site piezometer and tensiometer data. Comparison of predicted and field data suggests that the model gives acceptable, but by no means perfect, prediction of the landslide hydrology (see Figs 5a+b). Because of the way in which shallow landslide movement is activated (at a critical water-table threshold), the model could be calibrated in such a way as to capture threshold exceedence frequency of observed data. Initial testing of the model with observed climate data from the past thirty years has predicted an exceedence frequency that correlates well with historical data from the area (GSL, 1986).
a.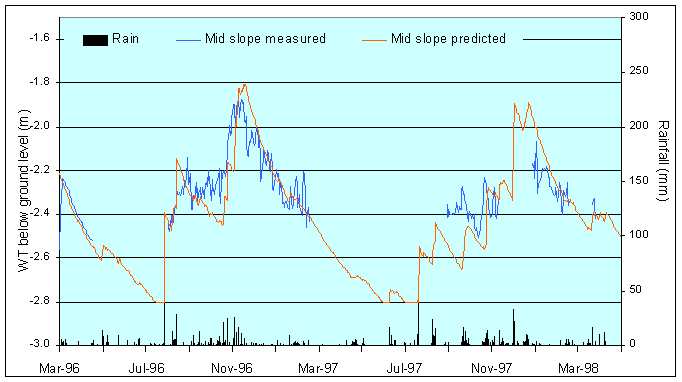
b.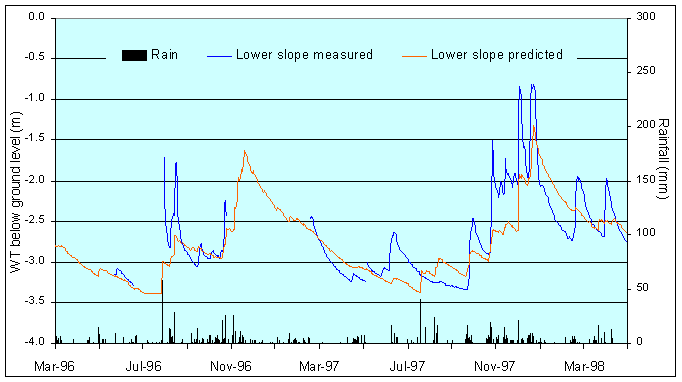
Figures 5a+b: Distributed model run for the Roughs test site for monitored period between March 96-98. Groundwater variation tends to be greater in the short-term for mid-slope areas (top), while longer-term variability is exhibited lower on the slope (below). This is reflected in the correlation between observed and predicted values, which varied between 0.78 in the middle of the slope to 0.82 on the lower slope.
The second generation of the U.K. Hadley Centre GCM (HadCM2) experiments have in broad terms successfully simulated the observed behaviour of the global climate system for the period between 1860 and 1990 (Johns et al., 1997; Mitchell et al., 1995). The data used here has been derived from the HadCM2 GS experiment, which represents increasing greenhouse gas emissions expressed as 1% per annum equivalent increase in CO2 concentration from 1990 to 2010, with negative forcing of sulphate aerosols (IS92a sulphur dioxide emissions scenario). Derived from a relatively coarse spatial grid, operating with a cell size of 3.75° longitude by 2.5° latitude (approximately 40,000 km2 in the U.K.), the data tended to be relatively inaccurate when compared with observed field data. For example, the mean yearly rainfall around the Hythe test site was predicted to be approximately 1,100 mm between 1960 and 1989, whereas the observed rainfall at the site was 740 mm (s.d. 91 mm). In order to convert the data into more realistic local temperature and rainfall data, the downscaling technique of Dehn and Buma (1997) was employed.
The data suggests that since 1861, precipitation at the Roughs will have risen by approximately 10% by the year 2100. While such a change in rainfall totals would doubtlessly have a marked effect on slope stability if not countered by a similar rise in temperature, a change in the shorter term variability might be just as significant. Indeed, precipitation tends to exhibit such short-term variability that it might be difficult to determine the effects of longer term change. The contrast between long and short term variation can be seen more clearly in Figure 6, which illustrates predicted precipitation between 1861 and 2100. In modelling with input data of this nature it would be wrong to assume that an increase in short-term landslide activity is a result of climate change, as in reality it may simply be a product of natural variability within the input data. This suggests that it may only be possible to make valid statements about landslide probability in the much longer term (c.100 years), when the effects of shorter term rainfall variation becomes relatively less significant.
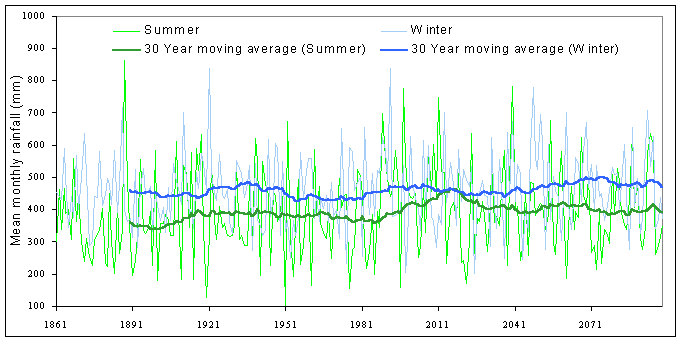
Figure 6: Predicted future mean monthly precipitation under HadCM2 GS climate scenario, with 30-year running average shown. (Summer: April to September; Winter: October to March).
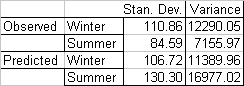
In order to assess the degree to which shorter term variability may be a function of the climate modelling and downscaling processes alone, comparison was made between observed and predicted precipitation. By comparing seasonal mean monthly data for the period 1900 to 1990 (Figures 7 and 8), it can be seen that while predicted winter rainfall is slightly less variable than observed, predicted summer rainfall is much more than actual (see Table 1). If this pattern were reproduced in climate predictions for future years we might expect hydrological models to over predict water table exceedence frequencies in the summer months.
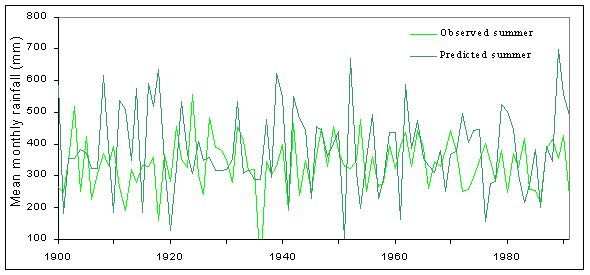
Figure 7: Mean monthly rainfall (summer): Comparison of variability exhibited by observed data (Sandling Park), and predicted (HadCM2 CS).
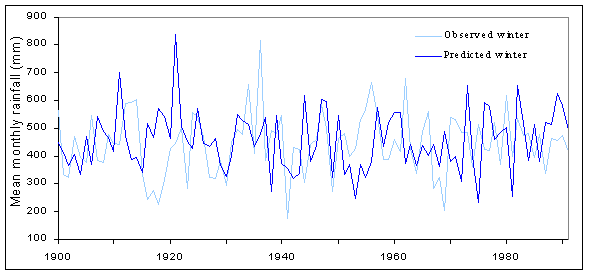
Figure 8: Mean monthly rainfall (winter); comparison of variability exhibited by observed data (Sandling Park), and predicted (HadCM2 CS).
The hydrological model described requires daily rainfall and temperature data. A simple weather generator was thus developed based on the statistical distributions of: the mean daily temperature; number of dry and wet days per month; and the amount of precipitation on rain days within each month. Based on a 127-year record of daily data from Folkestone, mean daily temperatures within each month were fitted to a normal distribution. Percentiles, rather than a statistical distribution, were used for daily precipitation in order to ensure that high magnitude events (95-100th percentiles) were not under-represented. For the relationship between the percentiles of P and normalised daily P (Pt / Pmean), a set of linear regressions (R2 between 83% and 99 %) were fitted between obvious break-points for each month so that:
Pt / Pmean = m X + c (8)
Where Pt is the observed daily P (mm) on a rain day, Pmean the mean daily P (mm), X is the percentile of the observed daily P and m and c parameters. Daily P series can be generated by replacing Pmean with the predicted total monthly P divided by the predicted number of rain days (N) from the GCM and X with a random number between 0 and 100. This method was used to generate a large number of continuous daily precipitation and temperature series for each GCM period. Rain days were clustered into a number of events per month, (determined by the monthly mean from the observed data). It was assumed that the variance of future intra-monthly distribution of precipitation and mean daily temperature will be the same as that of observed data.
In attempting to assess the impact of long term climate changes on landslide activity, the designed model was first run with observed climate data. The results were then compared with predictions using the derived GCM climate data. The difference between the results produced represents the impact of the perturbed climate; however, as already stated, if the variability of both observed and predicted data is relatively high, then any effects of actual climate change may be hidden within the effects caused by the natural variability of the data. It can be seen from the model predictions shown in Figure 9 that water-table exceedence frequencies (thus landslides), appear to decrease with time (due to increasing temperature and thus evapotranspiration). It also may be seen that for the period between 1960 and 1989, predictions of water table heights using observed and downscaled climate data are reasonably similar at higher water table thresholds for which the model was calibrated, but this is at the cost of accuracy at the lower (though admittedly less significant), water table heights. In addition to climate scenario predictions, vegetation input parameters to the model were altered in order to represent two contrasting vegetation types (Figure 10). Not unexpectedly the results indicated a reduction in ground water levels for coniferous vegetation type due to the higher levels of evapotranspiration.
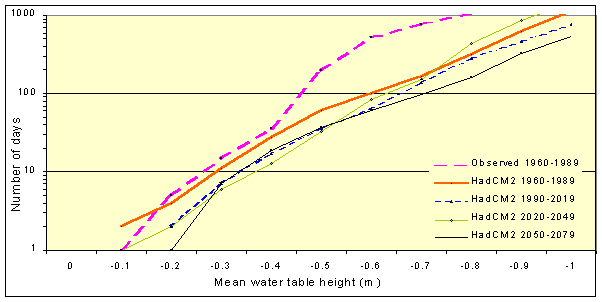
Figure 9. Predictions of water table exceedence frequencies for observed and predicted climate data
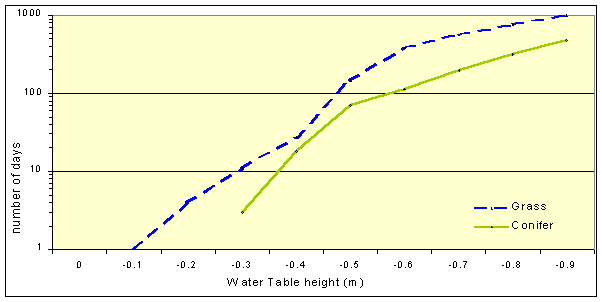
Figure 10. Predictions of water table exceedence frequency for observed data (1960-89), for two different vegetation scenarios.
Predictions of future mean water table heights for the Roughs test site indicate that an increase in temperature and evapotranspiration will, to a certain extent, mitigate the risk of increased landsliding through higher rainfall. Given the importance of short term precipitation variability to the build up of pore water pressure, however, greater representation or knowledge of how the model performs or reacts to rainfall is needed. Figures 11a and b indicate preliminary investigation of mean water table response to rainfall parameters and temperature. It can be seen that the model is more sensitive to changes in rainfall intensity than in total rainfall due to the bypass component representative of macro-pore flow.
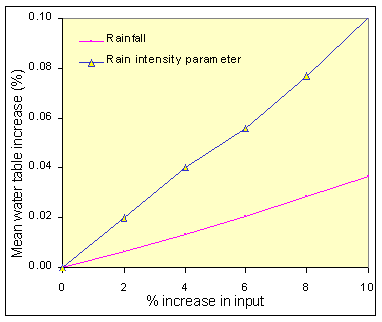
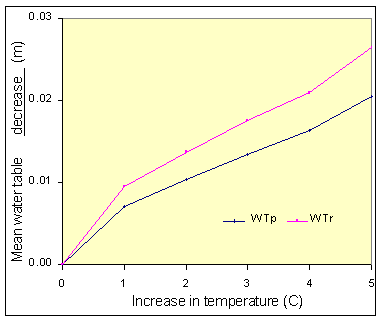
Figure 11a +b: Change in mean annual water table level relative to rainfall characteristics (left); and temperature (C), perched water table (WTp), regional water table (WTr), (right).
To conclude, it is recognised that though relevant hydrological processes are numerically modelled to an acceptable standard within the model, the results obtained describe changes to slope stability in relation only to rainfall and temperature. In order to account for the full effects of climate change, a better knowledge of the potential variation in relative humidity; net radiation; cloud cover; and regional patterns of rainfall intensity, duration and seasonality; are needed. As much of this information has yet to be quantitatively determined, the described model may be regarded as a best first estimate given the data available.
Initial stages of this research were funded through the European Communities Environment and Climate Program (1996-98): 'New technologies for landslide hazard assessment and management in Europe' (NEWTECH). Downscaled GCM data were supplied by Martin Dehn at Bonn University, derived from the Hadley Centre Link project. The authors also are indebted to Rens van Beek of Utrecht University, who provided DEMs and soil data analyses information for the Planes field site.
Anderson, M.G. and S. Howes, 1985. Development and application of a combined soil water-slope stability model, Q. J. Eng. Geol. London, Vol.18: pp. 225-236.
Bevan, K., 1979. A sensitivity analysis of the Penman-Montieth actual evapotranspiration estimates, Journal of Hydrology, 44: pp. 169-190.
Bevan, K.J. and M.J. Kirkby, 1979. A physically based, variable contributing area model of basin hydrology. Hydrological Sciences Bulletin 24, 1, pp. 43-69.
Bromhead, E.N., 1997. Landslides in The Roughs, a site on the Lower Greensand Escarpment in South Kent. NEWTECH, (unpublished workshop discussion paper).
Brooks, S.M. and K.S. Richards, 1994. The significance of rainstorm variations to shallow translational hillslope failure, Earth Surface Processes and Landforms, 19: pp. 85-94.
Brooks, S.M., M.G. Anderson, and A.J.C. Collison, 1995. Modelling the role of climate, vegetation, and pedogenisis in shallow translational hillslope failure, EarthSurface Processes and Landforms, Vol. 20, pp. 231-242.
Brunsden, D., M. Ibsen, E.N. Bromhead, and A. Collison, 1996. Final National Report, King's College London, UK. The temporal stability and activity of landslides in Europe with respect to climate change (TESLEC). European Commission Environment Programme (EV5V-CT94-0454).
Buma, J. and M. Dehn, 1998. A method for predicting the impact of climate change on slope stability, Engineering Geology, Vol.35, No.2-3, pp.190-196.
Coles, N. and S.T. Trudgill, 1985. The movement of nitrate fertilizer from the soil surface to drainage water by preferential flow in weakly structured soils, Slapton, S.Devon, Agriculture, Ecosystems and Environment, 13: pp.241-259.
Collison, A.J.C. and M.G. Anderson, 1996. Using a combined slope hydrology/stability model to identify suitable conditions for landslide prevention by vegetation in the humid tropics, Earth Surface Processes and Landforms, Vol. 21, pp. 737-747.
Dehn, M. and J. Buma, 1996. Modelling future landslide activity based on general circulation models - Method and uncertainties. Geomorphology. [In press.]
Dietrich, W.E., R. Reiss, Mei-Ling-Hsu, and D.R. Montgomery, 1995. A process based model for alluvial soil depth and shallow landsliding using digital elevation data. Hydrological Processes, 9, pp. 383-400.
Dikau, R., L. Schrott, M. Dehn, K. Hennrich, M.-L. Ibsen, and S. Rasemann, Eds., 1996. The temporal stability of landslides in Europe with respect to climate change (TESLEC). Summary Report, unpublished, Heidelberg, Germany.
Geomorphological Services Ltd., 1986. Review of research into landsliding in Great Britain: Report to the Department of the Environment [unpublished.]
Haneberg, W.C., 1991. Pore pressure diffusion and the hydrologic response of nearly saturated, thin landslide deposits to rainfall, Journal of Geology, vol. 99, pp. 886-892.
Intergovernmental Panel on Climate Change, 1990. Scientific assessment of climate change, WMO/UNEP, Geneva, Switzerland.
Johns T.C., R.E. Carnell, J.F. Crossley, J.M. Gregory, J.F.B. Mitchell, C.A. Senior, S.F.B. Tett, and R.A. Wood 1997. The Second Hadley Centre coupled ocean-atmosphere GCM: Model description, set-up and validation, Climate Dynamics, 13: pp. 103-134.
McKenny, M.S. and N.J. Rosenburg, 1993. Sensitivity of some potential evapotranspiration methods to climate change, Agric. For. Meteorol., 64: pp. 81-110.
Mitchell J.F.B., T.C. Johns, J.M. Gregory, and S. Tett S., 1995. Climate response to increasing levels of greenhouse gases and sulphate aerosols. Nature Vol. 376.
Montgomery, D.R. and W.E. Dietrich, 1994. A physically based model for the topographic control on shallow landsliding, Water Resources Research, Vol.30:4; pp. 1,153-1,171.
Ng, C.W.W. and Q. Shi, 1998. Influence of rainfall intensity and duration on slope stability in unsaturated soils, Quarterly Journal of Engineering Geology, 31: pp. 105-113.
Reid, M.E., 1994. A pore-pressure diffusion model for estimating landslide-inducing rainfall, The Journal of Geology, 102, pp. 709-717.
Rosenburg, N.J. and M.S. McKenny, 1995. Reply - Sensitivity of some potential evapotranspiration methods to climate change, Agric. For. Meteorol., 77:1 pp. 27-129.
Scotter, D.R., L.K. Heng, D.J. Horne, and R.E. White, 1990. A simplified analysis of soil water to a mole drain, Journal of Soil Science, 41: pp. 189-198.
Sugawara, M., 1995. Tank Model, in V.J. Singh, Ed., Computer models of watershed hydrology, Water Resources Publications, CO.
vanAsch T.W.J. and J.T. Buma, 1997. Modelling groundwater fluctuations and the frequency of movement of a landslide in the Terres Noires region of Barcelonnette (France), Earth Surface Processes and Landforms, Vol.22, No.2, pp.131-141.
van Beek, R., 1997. The influence of fissure-induced infiltration on slope stability: a conceptual model. http://www.geog.uu.nl/pcraster/exmod/stability/stability.html
van Beek, L.P.H., 1998a. Personal Communication on topographic interpolation techniques.
van Beek, L.P.H., 1998b. Suction Controlled Direct Shear Tests: The unsaturated strength of weathered Miocene Marl of the Alcoy Region (SE Spain), Geog. Dept. internal report (NWO-GOA 750.294.03), Utrecht University.
Van Deursen, W.P.A., 1995. 'Geographical Information Systems and Dynamic Models: development and application of a prototype spatial modelling language. Netherlands Geographic Studies, 190. See also http://www.frw.ruu.nl/pcraster.html
van Genuchten, M.Th., 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils, Soil Science Society of America, Vol. 48: pp. 892-8.
von Storch, H., E. Zorita, and U. Cubasch, 1993. Downscaling of climate change estimates to regional scales: An application to Iberian rainfall in winter time. J. Climate, 6: pp. 1,161-1,171.
Wade, S., A.J.C. Collison, and M. Dehn, 1998. Modelling the impact of predicted climate change on landslide frequency and magnitude in SE England, submitted for publication to Engineering Geology.
Wesseling, C.G., D.J. Karssenberg, P.A. Burrough, and W.P.A. Van Deursen, 1996. 'Integrated dynamic environmental models in GIS: The development of a Dynamic Modelling language. Transactions in GIS,1-1, pp. 40-48.