As far as the latter aspect is concerned, two more aspects must be specified:
| b1. |
the level of semantic complexity at which
the rules to be learnt are expressed (e.g. as general urban planning
principles or more specific modelling rules); |
| b2. | the "form" and the "criterion" by which the fitting between the learnt map and the target map is evaluated (in other terms, the "sensors" of the learning algorithm must be specified). |
On the side of the semantic complexity, in this initial steps of our work, we adopted the simplest solution, that is the direct expression of the rules in the same form as they act in the CA.
On the side of the sensors too, we choose the simplest solution, that is to accept or reject the rules depending on the matching (after their reiterated application) between the observed and the learnt state of a single cell of the automaton. More precisely, this matching (at single cell level) is analysed for a very great number of randomly selected cells and the rule is either prized (by increasing its level of "confirmation" and then its "strength") or punished (by decreasing its "strength") depending on the goodness of fit.
3.3. The computer structure of the prototype
The structure of the prototype is described in details in Papini and Rabino, 1997. It can be said here that, on one side we have a classic cellular automaton, while the other side presents a learning system (a typical classifiers system), divided into its three components: a rules generator, a rules "evaluator" and a module for the management of the system itself. The rules and the sensors are respectively the input and output interfaces of the automaton with respect to the classifiers system.
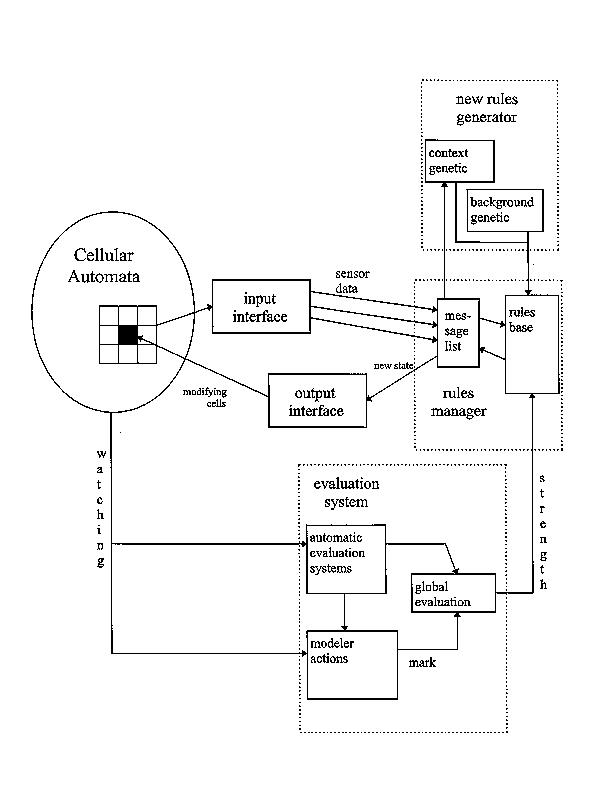
Moreover, it is to be specified that the rules generator is a genetic algorithm which "invents" new possible rules (to be evaluated) starting from previous rules, through the usual evolutionary mechanisms (random mutation, crossover, etc.). Therefore, the evolutionary character (beside that of learning) can be ascribed to the proposed cellular automaton.
Finally, we recall that the rules introduced in the model are rules of the kind IF ...THEN ... (condition-action rule, typical in classifiers systems) and codified by means of a bits string. The string defines the initial state of the cell, the state of its neighbouring, the presence (or absence) of other attributes of the cell and the final state of the cell, codified in the same way as the initial state.
4. The representation of the urban system
In the application of a learning cellular automata to an urban system, a particularly critical phase is represented by the writing out of the "textbook", that is of the contents and architecture of the information which are supplied for the automata.
Such architecture must consist of an efficient and effective description of both the spatial and functional structures of the urban system, as well as of its evolution, so that the model can read and interpret the evolution of such structures and deduce the rules which produced the transformation occurred in the considered time interval.
We describe the problems met in the description of such information structure and indicate the solution adopted in the application to Rome metropolitan area: these solutions are quite different from those that can be found in the classic applications of cellular automata urban systems.
4.1. The geometry of the cells
In the models conceived and/or applied in the US (since Lowry model up to C. A.) urban space has been usually disaggregated by adopting orthogonal grids.
This choice originates from the morphologic structure of the urban texture of the American cities and from the corresponding shape of the statistical elementary zones.
This representation of space turns out very useful in many contexts of urban modelling, ranging from the computation of distances and routes (in general, everything connected with the use of graphs), to all computer graphics problems, in which each square or rectangular sub-area can correspond with one or more pixels.
In Italy, such urban textures can be found only in the parts of cities built after the middle of the 19th century. The remaining, which is the most part, presents a spatial organisation and shape of buildings which cannot be represented by means of an orthogonal grid unless operating spatial deformations and data approximations so strong to be unacceptable, especially when working at a small and detailed scale, inside the urban "continuum".
Also the structure of distances and accessibility, on a network resulting from the overlay of centuries, is more complex than a structure in which the orthogonal grid prevails, with its regularity of blocks and of their size.
Therefore, we abandoned the idea of adopting an orthogonal grid for the representation of space, though aware of the increase of the level of complexity of the task, from both a semantic and a syntactic point of view. We then undertook the task of interfacing the C.A. with an algorithm which allows to represent a system in which cells be of any shape and assembled in any way.
By means of an appropriate software, it is then necessary to define and individuate adjacencies between such cells of any shape. We tackled this task being aware that it would not be useful only for the present application, but it would produce other relevant advantages, that are:
- to extend the application of the model to any kind of variables mapping, also at different scale, depending on the availability of data and on the level of detail which is to be adopted;
- to provide Cellular Automata with a wide transferability, in particular for C. A. built by different schools for different purposes.
4.2. The border problem
The problem of the identification of the boundaries of the system and that of its "closure" (i.e. how to model the relations between the "inside" and the "outside" of the system) is not new in urban modelling and has been always posed in the following terms:
| 1. | boundaries: how to determine the boundaries of the system in such a way to ensure that the most part of the considered phenomena and processes take place inside the system and therefore interactions with the outside be weak enough. |
The problem, which is included in the more general problem of the individuation of sub-regions, was often tackled by means of clustering techniques. (applied to interaction flows in a determined time section.
However, in the case at study, the spatial and functional interdependencies (the "rules"): are "found out" by the model; are rendered explicit only at the end of the learning process; are dynamic, as they are derived by the observed evolution of the system.
To overcome these problems, we must go through these steps: 1. arbitrary choice of the boundaries of a subsystem; 2. application of the C.A. and identification of the transformation rules; 3. comparison between simulated and real evolution; 4. if the fitting is not satisfying, modify the boundary and go back to step n. 2.
| 2. | "closure" of the system: how to model the relations, however weak, which exist between the inside and the outside of the system. |
In the field of the application of classic CA, the problem concerns the cells located on the border, and the solutions adopted most frequently are: the system is closed like a torus; "mirrors" are placed on the borders (Serra, Zanarini, 1990), in some cases, with different "reflecting capacity".
In the applications to urban systems, these solutions are not satisfying, because:
- the influence of the "outside" is not limited to the "border cells", on the contrary, it reaches to some distance from the "source" and then does not involve only the border cells (see, for instance, the application to Cincinnati carried out by White, Engelen and Uljie, 1993); this is also true as to the internal influences are concerned, therefore it is necessary to introduce some measure of the distance between cells in order to obtain a representation of spatial effects more realistic than that obtained by considering only the spatial relation between neighbouring cells;
- there is no reason to adopt (and there are many reasons not to adopt) the device of the introduction of "mirrors", which would imply to assume the existence of an improbable symmetry of the urban structure with respect to arbitrary points or axes.
In the application of our model, then, we choose to adopt a solution similar to that used for SIA models (see for instance Giangrande, Lombardo and Mortola, 1977).
It consisted in introducing "external zones": it was modelled their effect on the zones of the system, while it was not modelled the effect of the system on them.
This corresponds to the introduction of external "seeds" (Batty and Xie, 1994), which are "seen" by the C.A., but don't change during the dynamic evolution of the system and belong to the class of "fixed cells" (see the following chapter).
4.3 The representation of land use
4.3.1. The choice of the relevant classes of land use
As in any representation of urban and territorial phenomena, the problem is to find the best compromise between the quality of the representation, which requests a satisfactory level of detail, and the possibility of "reading" the representation, which implies problems of size of the data base.
In our application the limits derive from the CA "machine" which reads the rules, where a rule is the specification of all the land use transformations (and the number of transformations is proportional to the square of the considered land uses).
Therefore, the represented land uses must have the following requisites: a) to be in a number "bearable" by the algorithm; b) to be obtained by aggregations of urban activities homogeneous as to location behaviour; c) such aggregations must not "hide" the changes occurred, that is they must allow to catch the (most part of) change.
4.3.2. The individuation of the prevailing land use
On the basis of the above considerations , we analysed the 1981 and 1991 Rome Census data, referred to 5600 Census zones and to 674 types of activity.
The elaboration were made more complex by the awareness that, for a relevant part of the urban area, it was not acceptable to define only one prevailing land use (this problem was stressed also in Batty, Couclelis and Eichen, 1997), but it was necessary to introduce mixed land uses of the cells. We then had to define appropriate indicators and develop statistical analyses aimed to the individuation of thresholds which allowed to define, for each cell, the prevailing land use or the different mixes of land uses.
This analysis was developed following four consecutive levels:
1st level. Individuation of the cells with only residential use (R), with only productive use (P), with mixed use (M).
Indicator: IR = population / (pop.+total jobs)
Thresholds: IR > 0.9 Þ R; IR < 0.7 Þ P; 0.7 < IR <0.9
ÞM2nd level. Classification of the cells with only residential use (R) as medium-high density cells (Ra), medium-low density cells (Rb) and empty cells (V).
Indicator: IRD = inhabitants per hectare
Thresholds: IRD ³ 250 Þ Ra; 10 < IRD < 250 Þ Rb; IRD < 10 ÞV
3rd level. Classification of the cells with only productive use (P) for different economic activities (Pi); identification of further empty cells (V).
The economic activities were aggregated in such a way to satisfy the requisites described in 4.3.1:
1) TS: high tertiary 2) TI: common tertiary 3) IN: industry 4) SA: health services
Indicator: IPi = employed in activity i / total of employed
For each cell, it is chosen the activity with the higher number of employed (P1) and the next one (P2).
Thresholds: IP1 - IP2 > 0.1 Þ P1 is the prevailing activity, otherwise there is a mix of activities,
identified in the next level.
4th level. Classification of cells with mixed use (M) for different mixes (2 max).
The cells where there is a mix of residential and productive land use were identified at the 1st level and
the economic activity with which residential land use is mixed is defined by the maximum value of IPi
To identify the mix of activities, we assumed: IP1 - IP2 £ 0.1 Þ mix of P1 and P2.
As a consequence, the considered land use are 14 (see Table 1).
Table 1: The considered land uses
| Prevailing | Symbol | Mix | Symbol |
| Empty | V | Residence+high tertiary | M |
| High density residence | R | Residence+low tertiary | M |
| Low density residence | R | Residence+industry | M |
| High tertiary | P | Residence+health services | M |
| Common tertiary | P | High tertiary+common tertiary | P |
| Industry | P | High tertiary+industry | P |
| Health services | P | Common tertiary+industry | P |
| Ec. activities+health services | P |
Figures 1and 2 show - as one example - the 1981 residential land use and the transformation occurred between 1981 and 1991.
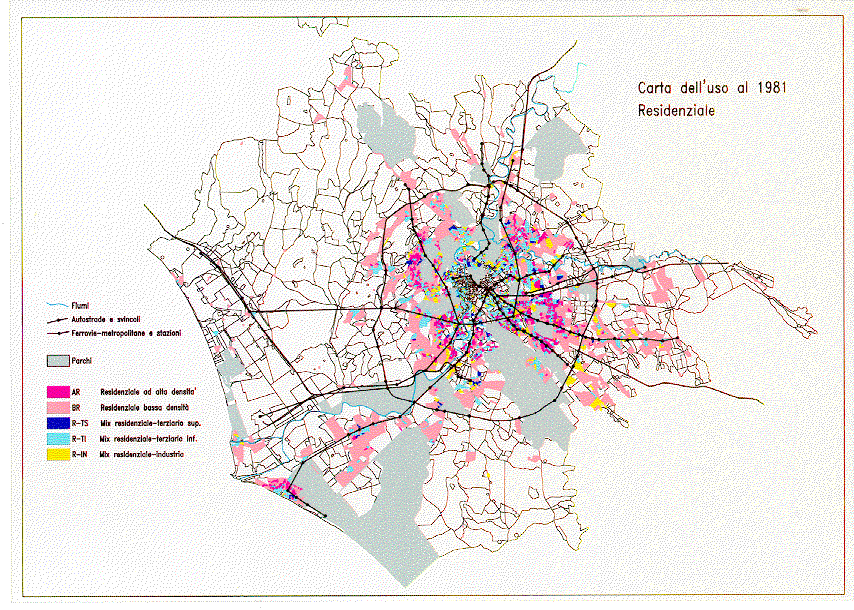
Figure 1: Residential land use in Rome (1981)
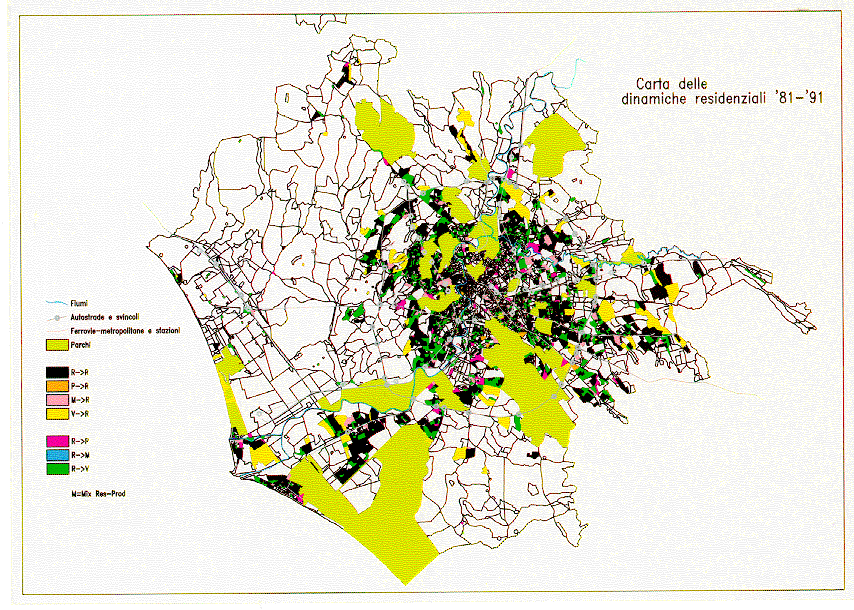
Figure 2: Residential land use transformation (1981-1991)
4.3.3. The "attributes" of the cells
It is to be considered that the general category here called "land use" includes land uses and/or characteristics (referred to points or to areas) which are fixed characteristics ("attributes") of the cells: they do not change, but influence the system dynamics.
Therefore, they are "seen" by the model as only "active" characteristics and not as "active and passive" ones.
The considered attributes can be distinguished as follow:
- attributes referred to points: they correspond to the presence in any cell of elements relevant from the point of view of accessibility; they are: 1) presence of railway or underground stations; 2) presence of accesses to the highway ring.
- attributes referred to areas: they characterise the whole surface of the cell. Some of them correspond to not changeable land use, therefore the cell becomes a "fixed" cell; they are: 3) parks and not transformable areas (by the General Plan); 4) sea (seed outside, see chapter 4.2); 5) other municipality (seed outside).
Other attributes do not make the cell a "fixed" cell; they are: 6) adjacency to a cell which presents one of the 5 attributes listed above; 7) historical centre (it influences attractivity and location costs).
These attributes are mapped in Figure 3; and the state of a (not fixed) cell is therefore defined by 12 bits: a) land use (4 bits); b) presence/absence of: station, access to highway, historical centre (1 bit each); c) adjacency to: station, access to highway, historical centre, park, outside "seed" (1 bit each)
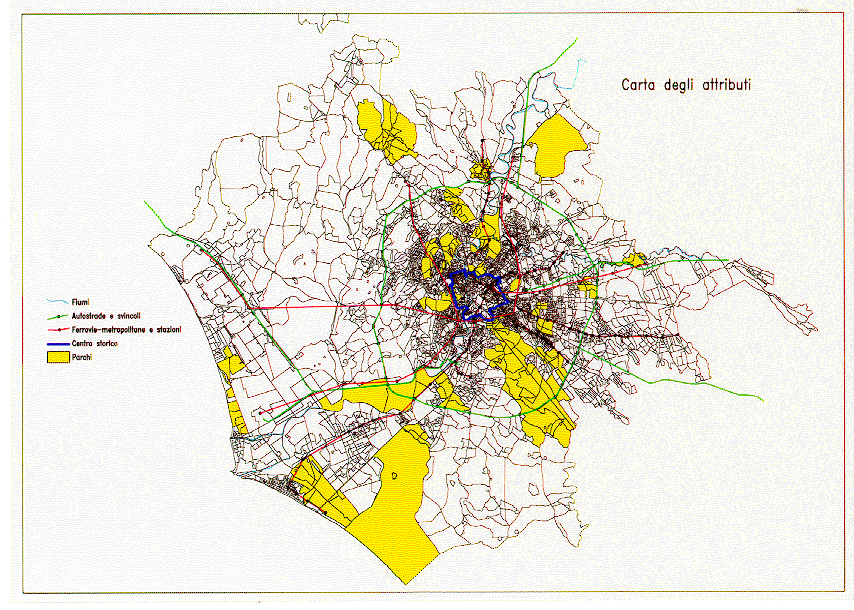
Figure 3: Attributes of the cells
4.4. Representation of distance effects
As said before, we think that it must be taken into consideration the fact that spatial influence reaches to some distance from the "source" and then does not involve only its adjacent cells. Therefore, unlike in the classic CA, in which spatial influence depends only on adjacency between cells, we introduced a continuous measure of the distance between cells, in such a way giving model the possibility of "studying" and introducing the idea of radius of influence of a cell and of its land use.
Indeed, in some applications of CA to urban systems there were introduced "bands" of "preferable" distance for the relations between different land uses. In these applications, though, it corresponded to the introduction of an additional rule, while, for our model, the distance matrix is an additional information whose role and importance is to be learnt.
However, as the use of a distance matrix with a size of 5600x5600 elements would produce difficulties in the computations and as it is likely that the spatial influences do not have relevant effects beyond a certain distance, we considered only distances not greater than 4 km. In other terms, it correspond to the adoption of an "enlarged adjacency", while the strict adjacency is used only as far as the influence of "attributes" is concerned.
In the experiments, we adopted geometrical distances between cells, in order to simplify the task of the preparation of the data base.
5. Possible structures of sensors
In synthesis, in our case, the problem is "to tune in" model sensors, designing its structure in such a way that it is able to read and interpret different typologies of phenomena and of evolutive structures. Table 2 lists some examples of phenomena and of evolutive structures of the system, with increasing complexity, on which sensors of our learning C.A.can be tuned in.
In this first simplified application to Rome urban
system, model was tuned in the recognition of both inertial and
dynamic behaviours and in the effects produced on each cell by
the status of adjacent cells (see the symbol "*"
in Table 2), while the effect of a continuous measure of distance
between cells was not introduced in the experiment described here.
Table 2: Examples of phenomena recognisable by the model
| Dynamic behaviour | * Inertia
* Change |
| Local effects | * Imitative
* Complementary Competitive Hierarchical . . . . . . . |
| Field effects | Accessibility
. . . . . . . . . . |
| Recognisable structures | Global level structures |
6. The first results
About 300 rules of land use transformation were identified, each of them can be evaluated through its "strength" by ordering them according to decreasing values of such parameter. If we take into account the first 15 rules, we can say that model learnt, beside the existence of a certain level of inertia of the system, that the most part of the transformations took place in peripheral areas and that the urbanisation phenomena took place in the cells with a good level of access to the public transport network and/or to the highways and in those with a good environmental quality (adjacency to parks).
The results of learning process can be synthesised in the following way:
|
| Cells land use (1981):
| In the neighbouring of:
| changed as:
| strength:
|
| A)
| Empty
Low density residence
| # Railway stations
#*Highway accesses * Parks # Other municipalities-
| Low density residence
Resid.+Com. tertiary
| Very high
Med. high
|
| B) | Low density residence | Sea | Industry | Med. high |
| Low density residence | Tertiary mix | Med. high | ||
|
| Empty
Empty
|
| Residence+Industry
Residence+Tertiary
| Med. high
High
|
| C)
| Empty
| Parks
Highway accesses
| Health services
| High
|
These rules concern mainly areas located in the periphery of the urban system; in particular:
- The symbol "#" indicates peripheral
zones (identified by presence/adjacency to highway accesses) and
some of them border on other municipalities. In this latter case
the model identified the trend of Rome urbanisation to trespass
the boundaries of its municipal territory. Moreover, in these
zones appears a mix of residence and tertiary, showing an evolution
towards an urbanisation more "mature" than in the other
cases.
The symbol "*" also indicates peripheral zones, but located in a good environmental context (identified by adjacency to parks). Such characteristic, coupled both with the relevance of the presence/adjacency to highway accesses and with the no relevance of stations, could correspond to classes of population with a medium-high income.
- Coastal areas, that actually showed a certain liveliness as
to change and urbanisation growth.
- They are specific cases, concerning zones were hospitals were built in peripheral areas (identified by presence/adjacency to highway accesses) with in a good environmental context (adjacency to parks).
The evolution rules identified were then applied to produce a simulation of the system. By comparing observed and simulated urban structure, the following level of error can be observed:
- being 5374 the cells which could change, the errors made were 219, that is 4% of cells were wrongly simulated;
- the inertial behaviour of the system (i.e. "no change") shows a level of error lower than the medium one;
- levels of error higher than the medium one are produced by an over rating of the new urbanisation phenomena (i.e. transformation from empty to residential land use) and by an over rating of the productive activities in some cells, where such activities become prevalent with respect to residence.
- the spatial distributions of the errors is quite even in the territory (see Figure 4), therefore there are not parts of the system whose behaviour was misleading as to the learning process.
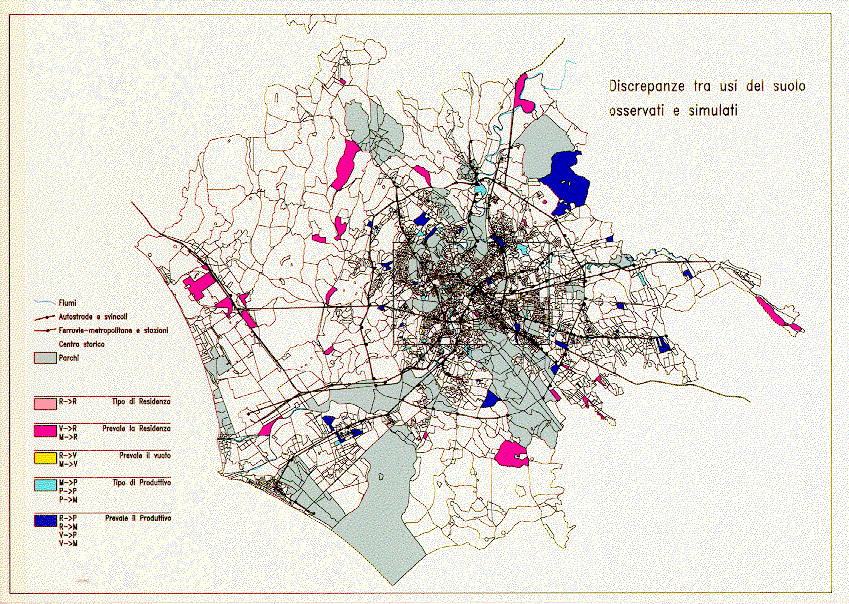
Figure 4: Errors in land use simulation (1991)
6.1 Concluding comments
In conclusion, in our opinion, this first experiment with a complex and totally new tool such as a learning urban cellular automata produced very encouraging results, enough to contradict a recent statement made by Batty and Xie (1997):
As to the research prosecution, considering the simplifications adopted, not so much for the system representation (however, in next experiments, we will introduce real estate price, for instance) as for the sensors' structure of the CA, it will be oriented to the re-designing of the sensors, aimed to their sharpening, in order to allow the recognition of more complex phenomena, such as those indicated in Table 2.
References
Allen P.M., (1979) A dynamic model of growth in a central place system. Geographical Analysis, 11, 256-272.
Batty M., Couclelis H., Eichen M. (1997) Special issue: Urban systems as cellular automata. Environment and Planning B, 24, 159-164.
Batty M., Xie Y. (1994) From cells to cities. Environment and Planning B, 21, 531-548.
Batty M., Xie Y. (1997) Possible urban automata. Environment and Planning B, 24, 175-192.
Besussi E., Cecchini A. (1996) Artificial Worlds and Urban Studies, DAEST n.1, Venezia.
Giangrande A., Lombardo S., Mortola E. (1977) Calibratura del modello di Lowry estesa alla variabili di attrazione zonale: applicazione ad una sub-area dell'Alto Lazio. Atti delle Giornate di Lavoro AIRO. Parma, 731-751.
Klosterman R.E. (1994) Large-scale Urban Models: Retrospect and Prospect. Journal of American Planning Association, 60, 3-6.
Lombardo S. (1995) Note sulla valutazione dell'incertezza nei sistemi complessi. Atti del Seminario Internazionale "La città e le sue scienze", AISRe, Perugia, 86-102.
Occelli S., Rabino G.A. (1997) Un modello urbano operativo per la città post-fordista. Atti della XVIII Conferenza Italiana di Scienze Regionali, AISRe, Siracusa, 435-455.
Papini L., Rabino G.A. (1997) Urban Cellular Automata: an evolutionary prototype, in ( Bandini and Mauri eds.) ACRI '96. Proceedings of the Second Conference on Cellular Automata for Research and Industry. Springer , Berlin. 147-157.
Rabino G.A. (1995) Tesi di pianificazione urbanistica. Atti del Seminario Internazionale "La città e le sue scienze", AISRe, Perugia, 46-66.
Sanders L., Pumain D., Mathian H., Guerin-Pace F., Bura S. (1997) SIMPOP: a multi-agent system for the study of urbanism. Environment and Planning B, 24, 287-305.
Serra R, Zanarini, G. (1990) Complex Systems and Cognitive Processes. Springer Verlag, Berlino.
White R, Engelen G., Uljee (1993) Cellular automata modelling of fractal urban land use patterns: forecasting change for planning applications. paper presented at 8° European Colloquium on Theoretical and Quantitative Geography, Budapest.