State of the Art Exploratory Spatial Data Analysis Tools

SPIN!-project Report

Andy Turner

This project report was drafted in the first year of the SPIN!-project to brief partners and prepare for a report deliverable due as part of Work Package 5. The report was placed online in August 2003 along with a follow up report concerning the State of the Art Geographical Data Mining that was drafted in January 2003. This report is also available as a word document.

Fundamentally this report details what exploratory spatial data analysis (ESDA) involves, outlining the special roles that inductive analytical techniques and visual environments play in supporting it.  The report is based on a search for and the use of a variety of computer software that supports ESDA, discussions with users and developers of these tools, an examination of relevant literature and a careful consideration of all the available expert opinion.  The report aims to encourage the development and integration of appropriate ESDA functionality in the spatial data mining system for data of public interest we are building (SPIN).  It does not review the technology currently being integrated in SPIN, rather it provides an overview of the functionality of other available ESDA tools and suggests what of this and what additional functionality could further enhance the ESDA capabilities of SPIN.

1. Background and Introduction

Data mining systems (DMS), geographical information systems (GIS), mathematical software packages (MATHS), statistical software packages (STATS), and bespoke software technology are complementary tools with wide ranging functionality that can be applied to analyse data that relate to real world systems.  The spatial data mining system we are building (SPIN) is an attempt to integrate much of the useful functionality of these tools in a highly extensible, open, internet-enabled plug in architecture that enhances ESDA capabilities for data of public interest.  This report describes a number of these ESDA tools and suggests what functionality to integrate in SPIN in order to enhance its ESDA capabilities.

The main aims of the SPIN!-project are:

• To develop an integrated, interactive, internet-enabled spatial data mining system for data of public interest.
• To improve knowledge discovery by providing an enhanced capability to visualise data mining results in spatial, temporal and attribute dimensions.
• To develop new and integrated ways of revealing complex patterns in spatio-temporally referenced data that were previously undiscovered using existing methods.
• To enhance decision making capabilities by developing interactive GIS techniques, which provide an integrated exploratory and statistical basis for investigating spatial patterns.
• To deepen the understanding of spatio-temporal patterns by visual simulation.
• To publish and disseminate geographical data mining services over the internet.

This report does not review the technology currently being integrated in SPIN.  Instead it aims to increase awareness of the special nature of spatial data, space-time data and geographical information, outline the problems concerning geographical data mining (GDM), describe the utility of available ESDA tools, and suggest some ideas for developing the analytical capabilities of SPIN.  Table 1 lists some of the special features of geographical information.

More basic than geographic information is spatial data, which is data attributed to a point line area or region defined by some geometrical system.  Geographical data is spatial data that also relates to some period or periods in time.  The spatial reference relates to some three-dimensional region on or near the surface of the earth that is abstracted in some simplified form.  Often a projection is used to cope with the curvature of the earth surface so that data can be viewed as flat surface.  Different projections distort distance area direction and orientation in different amounts using different surface constraint.  Some projections are designed to minimise a specific type of distortion all over the map, but this is very difficult and no matter what is done there is distortion which tends to vary over the map and be greatest at its extremes.  There are many different types of projections and various ways of transforming geographical data from one to another.  Projection functionality is available in most standard GIS.  Many geographical data sets relate to small spatial regions for which the effects of the curvature of the earth are negligible compared to the effects of study area definition.  For small area data the problems of map projection do not take effect until data sets are merged to form significantly larger regions.

Geographical data can be spatially referenced in a number of ways.  Commonly it is either referenced irregularly to points lines surfaces or regions (using a co-ordinate system with a specified origin and level of precision), or it is represented by a regular regionalisation or fixed set of evenly spaced measurements with an implicit topology (for a specified origin and spatial resolution).  These are often referred to as vector data and raster data respectively.  Functionality for converting data from one form into another is available in most standard GIS.  Most standard GIS can manipulate display and analyse both types of data but they have tended to specialise in methods relevant to one or the other.  Much geographical data is two-dimensional and relates to small areas on or near the surface of the earth.  However, there is an increasing amount of data collected and referenced spatially with three-dimensional co-ordinate systems (e.g. soil data, seismic data, hydrological data and climatological data) nd increasingly two-dimensional data is being made three-dimensional by adding a height variable.  For example a two-dimensional set of lines representing rivers can be draped over coincident digital terrain models to produce more useful three-dimensional sets of lines.  Many GIS now include three-dimensional data handling display and analysis functionality.

As mentioned above, geographic data is often also temporally referenced, that is, it is collected and related to a specific period or to various periods in time.  Often the temporal reference is fixed and implicit for a set of spatial data, but increasingly it is an explicitly recorded variable.  Space-time referenced data are sometimes referred to as tri-space data, that is, they may have a single or multiple set of attributes and they relate specifically to region(s) in space and a period(s) of time.  Really, GDM goes beyond ESDA and spatial data mining where time is either fixed or regarded no differently to any other aspatial variable.  GDM involves searching for and generalising patterns and relationships in tri-space data, which is notoriously difficult, see Openshaw (1998).

ESDA and spatial data mining are terms that appear frequently in geographical contexts, but it is worth while remembering that it is a generic term that might be used in other areas of spatial science.  Fundamentally, ESDA demands an awareness of the special nature of spatial data and the exploratory approach to data analysis.  The exploratory approach involves visualising data and generalisations (derivatives) of them in tables, graphs, maps and various other types of display.  Human analysts interpret these displays to gain an appreciation of the nature of the data, which often helps them to define interesting subsets of data and guide the search for interesting and potentially useful patterns and interrelationships in it.  ESDA and data mining in general are interactive and iterative search processes where patterns and relationships in data are used to refine the search for more interesting patterns and relationships.  With a very large amount of data, ESDA is equivalent to spatial data mining.  To clarfy the terminology, geographical data mining (GDM) is spatial data mining of data relating to geographical processes, and spatial data mining is ESDA involving very large quantities of spatial data.  GDM, spatial data mining and ESDA are essentially very similar activities that can begin without any hypothesis to test regarding the nature of patterns in the data and how they relate to real world processes.  The basic idea is to encourage the data to express themselves in order to identify interesting patterns that help generate hypotheses about the processes underlying them in the real world.

Data generated theories or models of a process can only be partly corroborated by empirical measurement, there is always some interpretation going on as to the processes at work.  In an exploratory data led approach to theory generation it is very important to try and keep as separate as possible data for building and data for validating models.  As well as this it is also advisable when developing tools to find specific patterns that their capabilities are tested using synthetic data where the patterns are known to some extent.  Further to this there is a need to interpret the quality of data going in and results coming out.  It is often a good idea to test how likely any patterns observed in the data are caused by error, and how sensitive observed patterns are when random noise is added to the data.  In a way the null hypothesis in the exploratory approach is that all data patterns are a consequence of randomness and data error.

DMS, GIS, MATHS, STATS, bespoke programs and computer operating systems are used in conjunction for ESDA and spatial data mining.  Although each different type of software is specialised for a particular use there is an overlap in functionality between them albeit that some are faster and more efficient than others and can cope better with large volumes of data.  Individual software tools are becoming increasingly flexible and there is increasingly less need to have many different tools to analyse data in general.  The remainder of this section introduces GIS, DMS, MATHS and STATS in turn, then outlines the remainder of this report.

Standard GIS packages offer only very basic sorts of data mining functionality and nothing in the way of inductive analysis techniques that are the core functionality of DMS.  Standard GIS also offer only very limited statistical functionality and support only fairly basic mathematical operations on tables of data.  Perhaps the most important thing to appreciate about standard GIS is that they tend to be limited to fairly basic forms of spatial analysis, (perhaps with the exception of network analysis at which some are quite sophisticated).  A further criticism of most standard GIS is that they do not offer linked dynamic display environments that can be used to search for interesting data patterns and relationships.

However, in the last few years a new generation of GIS has been emerging which do provide linked dynamic display environments.  This new generation have mainly been developed separately from the more standard proprietary GIS by academic researchers who already have these tools available.  Consequently the new generation do not have much of the more standard functionality, but they do enhance ESDA capabilities by facilitating an interactive exploratory and graphical approach to analysing spatial data.  Like standard GIS - new generation GIS still lack data mining tools and useful geometry related spatial analysis functionality, but this should not detract from what they do provide.  LiveMap, CDV, SAGE, and GeoTools are examples of new generation GIS that are described in Section 3.

DMS have developed largely unconnected to GIS research and offer a range of useful data analysis tools.  DMS aim to provide user-friendly interfaces and visual programming environments that promote an interactive search for patterns in data.  The majority of DMS are equipped to analyse multivariate time series data taking account of the linear or cyclical transgression of such data.  Unfortunately, most fail to recognise the need to treat spatial data and spatial variables any differently from their aspatial relatives.  Contemporary DMS do not offer an easy to use highly automated push button technology and instead rely greatly on the users understanding of how the data represents reality and how the available tools can be sensibly used to analyse it.  Due to the nature of the data mining industry there are a vast number of commercial systems that exist and a vast amount of hype surrounding them.  This means that in descriptions of the systems there are many exaggerated and misleading claims about their caabilities and a lack of information about their weaknesses and indeed the functionality of the tools they contain and how they work.  The systems themselves are also very expensive and some are tuned to work on very specific hardware making them hard to evaluate and compare.  Many DMS developed primarily as interfaces to neural networks with some kind of data input and display functionality.  The majority of packages also contain other methods for classifying data, tools for linear and logistic regression, for generating decision trees, for association rules detection and for sequence discovery.  Section 2 first outlines the functionality and capability of contemporary DMS in more detail, then outlines GeoMiner, which is the only spatial data mining system that was found during the search for them.  It falls some way short of reasonable expectations of such a system.

In MATHS the most useful additional spatial analysis functionality relates to geometry and fuzzy logic.  Geometry forms the foundations of spatial analysis and is a vast branch of mathematics and thus cannot be detailed here.  Capability to construct and use geometrical shapes for generalising spatial data is undoubtedly a requirement for SPIN.  Fuzzy logic based methods of classification, prediction and inference are more relevant and are outlined in Section 4.

STATS support statistical inference methods that are commonly used for analysing the distribution of aspatial variable values.  There is a problem applying many of these methods sensibly to spatial data due to the inherent assumptions about the nature of the data on which they are based.  This does not mean that they cannot be useful for some forms of spatial analysis, only that the results of applying these methods should be interpreted cautiously.  Other statistical methods, which do not infer the nature of variable distributions or data dependencies are more relevant to ESDA and GDM.  There are some spatial statistical methods can be applied to analyse spatially irregular or sampled data, but most only work well with spatially regular data.  One recipe for spatial statistical analysis is outlined here: The first step involves plotting all the data for each variable and assessing whether it comes from a stationary random field by checking for stationarity (a constant mean within specified regions across he study region).  If a spatial variable is found not to exhibit stationarity then various trend surfaces that relate nearby values of the variable are fitted and assessed by testing the residual differences between observed and expected values for stationarity.  Having taken away the univariate trend the analysis proceeds by mapping and attempting to correlate variables in the data set to form more complex models of spatial association.  In fact, few STATS facilitate this kind of spatial statistical analysis, an exception is SpaceStat that is described in Section 5.  Much of the hypothesis testing functionality concerning probability distributions commonly found in STATS is difficult to apply sensibly in a spatial data mining context due to fundamentally flawed assumptions.  Local indicators of spatial association (such as Geary's C and Moran's I) and local statistics (like the mean, standard deviation and correlation coefficients) are useful and so SPIN should provide ways of computing these for various spaial subsets.  Testing patterns against randomness and using bootstrap methods is of course also very relevant to SPIN.

Altogether there are a vast number of tools that can be used for ESDA and spatial data mining.  Perhaps one of the most challenging problems in developing SPIN concerns what functionality to include, what order to develop it in and what levels of automation to provide.  This review is a reference point in addressing these issues aiming to provide a synoptic overview rather than a comprehensive and detailed evaluation of what is currently available.  The main assumption of this report is that many end users will not have expertise in the statistical or spatial sciences but will hope to perform some sort of geographical data mining.  The reader of this report is assumed to be aware of the functionality available in proprietary GIS and the proposed SPIN.  Section 2 describes the exploratory or data mining approach to the analysis of large spatial databases again and outlines the core functionality of DMS briefly reviewing Clementine, Intelligent Miner for Data and GeoMiner.  Section 3 outlines some of the new eneration GIS that offer linked visual display environments including CDV, SAGE, LiveMap, GeoTools and GeoVista. Section 4 is concerned with fuzzy logic.  Section 5 outlines two other spatial STATS packages SpaceStat and S+ and a bespoke ESDA tool called GWR.  Finally, Section 6 presents a summary.

2. ESDA, data mining and spatial data mining tools

To recap, spatial data mining systems are essentially ESDA tools.  ESDA and spatial data mining involve an interactive search for patterns or regularities in spatial data.  The processes could begin by visualising data in maps, graphs, charts, plots and tables.  Following this some form of data classification and some form of variable prediction could be performed, the results visualised and the predictions and models tested in some way.  This process could continue until something interesting or useful emerged or until the analyst became satisfied that the data contained no detectable patterns of interest.

Vastly increasing quantities of spatially referenced data of all kinds are being collected all the time, much of it relates to geographical and geophysical processes and much of it is of public interest.  This has led to data rich but theory poor environments that fundamentally require an exploratory rather than a confirmatory hypothesis driven approach.  Tools needed to help generalise and visualise patterns in these data have begun to emerge, but tools that use all the available data at the highest level of resolution with a minimum of preselection as yet have not.

ESDA tools, in particular SPIN, should be designed to be end-user friendly in that the results should be understandable and capable of being safely used by people who do not have higher degrees in the statistical or spatial sciences.  Outputs from the tools should aim to stimulate the imagination.  If there are patterns hidden in spatial data or indeed relationships encrypted in spatial information then the ESDA tools in SPIN should help users to find them by at least pointing them in the right direction.  An important goal is to provide an end-user friendly ESDA environment containing highly automated analysis tools that are easy to apply, whose visualised outputs are easy to interpret and whose techniques are explained in simple terms so that non-experts can understand how they work.

It is important to appreciate the vast difference between exploring a manageable small data set with few variables and the need to perform the same process on massive databases (with many more cases) and possibly high levels of multivariate complexity.  Manual graphical exploration of multi dimensional spatio-temporal data does not scale well, that is, the larger the volume of data gets - the greater is the need for generalisation and automated analysis methods.

There are a number of data mining tools designed to assist the process of exploring large amounts of data in search of recurrent patterns and relationships.  Many developers and users of these tools appear to believe that their tools will work with any and all data regardless of its subject origins.  This overlooks the features of geographical information that make it special that were summarised above in Table 1.  GDM is a special type of data mining that has to take into account the special features of geographical information, the rather different styles and needs of analysis and modelling relevant to the world of GIS, and the peculiar nature of geographical explanation.

It can be argued that conventional data mining tools are still useful, in the same way that conventional statistical methods can be applied to spatial data.  However, the view expressed here is that conventional statistical techniques and conventional data mining tools are not sufficiently focused on, and tailored to, the special needs of geographical analysis today.  Most data mining packages offer: exploratory data analysis tools to display data in various ways; most multivariate statistical methods including linear and logistic regression; various classification and modelling tools, such as decision trees, rule induction methods, neural networks, memory or case based reasoning; and, sequence discovery (time series analysis).  Many of these methods can be usefully applied to spatial data.  For example, data reduction tools, such as multivariate classification, can be useful as a means of summarising the essential features of large spatial data sets.  Modelling tools such as neural networks and decision tees can be readily applied to some geographic problems.  Although it can be argued that these methods ignore some of the special features of geographical information outlined in Table 1 - they can still be usefully applied to spatial data.

Conventional DMS have no mechanism for handling location or spatial aggregation or for coping with spatial entities or spatial concepts such as a region or circle or distance or map topology.  What are therefor needed are new types of data mining tools that can handle the special nature of spatial information.

Most analytical functionality available in DMS are simple extensions and generalisations of techniques used for decades. The core functionality in most DMS is based on artificial intelligence and other techniques that can be set to search for patterns and trends in large volumes of data.  Neural networks (NN) are universal approximators that mimic the workings of animal nervous systems that learn to classify and generalise patterns in their local environments.  They have powerful pattern recognition and generalisation capabilities derived from their ability to learn to represent complex multi-variate data patterns.  There are three main types of neural network commonly used in research; the multilayer perceptron, the learning vector quantisation network, and the self organising map.  Multilayer perceptrons are perhaps the most common, but the majority of DMS also incorporate some form of self organising map.  Genetic algorithms (GA), also called evolutionary algorithms, constitut a set of powerful global search heuristics that are also biologically inspired.  They mimic the basic idea of the evolution of life forms as they adapt to their local environments over many generations.  Both NN and GA provide a means of approaching highly complex search problems by simulating in the computer the biological process of natural selection and we should aim to incorporate them in SPIN.

Clementine

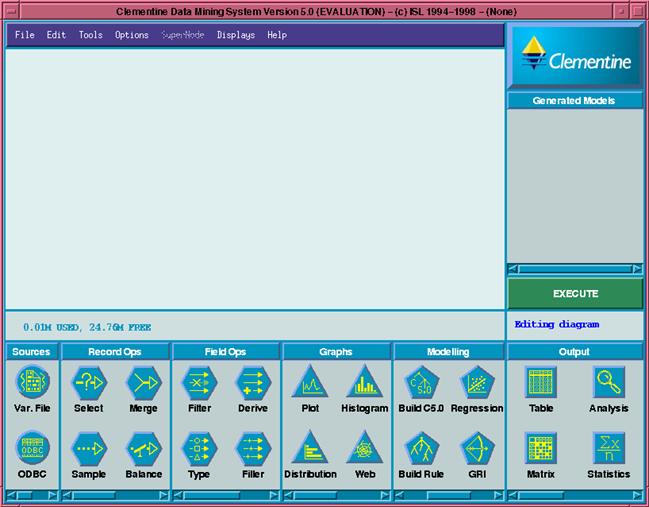
Clementine Data Mining System (Clementine) was originally developed by Integral Solutions Ltd who were recently bought by SPSS.  SPSS offer various training courses, provide a support service for users of Clementine and undertake consultancy work.  Clementine has a user friendly visual programming GUI for developing data mining applications, see Figure 1 below.  There is a menu across the top which can be used to load and save features specific to the data mining application, set parameters, run modelling scripts and load a basic help system.

Clementine stores input data as a table and most operations are performed sequentially record by record.  The skeleton of a data mining application is represented by a set of stream diagrams which are usually constructed in the GUI model building pallet but can also be defined using CLEM, the Clementine macro modelling and scripting language.  Streams can be saved and loaded from file and can be executed more efficiently in batch mode using modelling scripts.  All Clementine streams are comprised of a set of nodes which are linked together to form a sequence of operations on a table of data.  A variety of nodes can be selected from the node pallet at the bottom of the GUI and connected into a stream, the following types of node are available:

• Source nodes: These are used to define the input data and read it into a table.
• Manipulation nodes: These are either used to perform operations on records (rows of data) or on fields (columns of data).  They are used to define the field type, derive new fields, filter out unwanted fields, join or merge tables together, select records, append records, sample records, sort records, or balance records (by either generating or deleting records under specific criteria).  (Whether operating on rows or columns of a table, data is read record by record, so in general field operations are far less efficient than record operations.)
• Graph nodes: These are visual display including histograms, bar charts, point or line plots and web diagrams.
• Modelling nodes: These include; a train_net_node from which 5 different types of supervised neural networks can be specified, a train_kohonen_node to perform unsupervised classification into a specified number of classes using the Kohonen self organising map (SOM), a train_kmeans node to perform Kmeans classification, a simple linear regression node and four different types of build rule nodes which either produce decision trees or association rule sets.
• Generated model nodes: These are the models generated upon execution of a modelling node.
• Output nodes: These include a node for calculating summary statistics and the correlation between specified variables, a node for generating standard output files, a node for creating a matrix output, a node for analysing the fit of a model, and a node for setting global parameters for a stream.
• Supernodes: These are parts of a stream catenated into a single icon for which internal parameters can be set. Streams that split into multiple streams cannot be encapsulated in a supernode.

A useful feature, particularly for streams that split into multiple channels, is that as the data table passes through a node it can be cached (stored at that node).  Nodes, streams, caches, generated models and modelling scripts can be individually saved and loaded from file as can the state of any Clementine session which stores the stream, any generated models, current parameter values and the modelling script associated with the stream.  Clementine has several types of parameter including slot parameters, supernode parameters, stream parameters and global parameters.  Slot parameters are used to control some of the editable characteristics of nodes, whereas, supernode parameters, stream parameters and global parameters are more like declared variables used in conventional programming.  A major limitation of the system is that data or parameter values cannot be passed back to a modelling script from the stream it is executing.  This means that Clementine cannot automatically perform many potentially ver useful recursive operations.  First impressions of Clementine are that the GUI is tidy, elegant and intuitively laid out, but its data manipulation functionality and visualisation capability are basic.  For more information on Clementine refer to SPSS.

Figure 1. Clementine GUI

Intelligent Miner

The IBM intelligent miner for data (IMiner) is described by IBM as: “... a suite of statistical, processing, and mining functions that you can use to analyse large databases.  It also provides visualisation tools for viewing and interpreting mining results…” IMiner provides access to on-line analytical processing functions for cleaning and re-arranging data in a similar way to the data manipulation nodes provided in Clementine.  These processing functions enable missing values to be defined, rows and columns of data to be filtered, data to be discretised into specific ranges, randomly sampled, aggregated, joined, and converted to lower or uppercase.  IMiner enables you to specify cyclic fields where values have a cyclical relationship to each other such as days of the week.  IMiner can also create taxonomy objects to define a hierarchy of relations between data categories.  Each item of a data table can be categorised and corresponding relations between these item categories can be used to define associations and sequential patterns.

The standard statistical functions available include bivariate statistics, factor analysis, linear regression, principle component analysis, and univariate curve fitting.  The following IMiner data mining functions are available:

• Associations mining function - designed to reveal associations that one set of items in a transaction implies about other items in that transaction (where a transaction is a row of a data table).
• Sequential patterns function - designed to discover patterns over time.
• Tree induction - a binary decision tree based on the SLIQ algorithm that can handle both numerical and categorical data attributes.
• Neural classification and prediction - these are either radial basis function nets or standard multi-layer perceptron type neural nets capable of supervised training using a back propagation algorithm.  These create sensitivity analysis reports that rank the input fields according to the degree of relevance or accuracy to the resulting classification or prediction.
• Neural clustering - this is a Kohonen net or self organising map (SOM) classifier which is a neural network in which the neurons iteratively compete to represent the data classifying it into clusters.
• Demographic clustering - this is similar to Kmeans but slightly more sophisticated in that the user can weight specific fields or values and can treat outliers in a number of different ways.

These functions have been developed to exploit RS/6000 SP hardware (configured by IBM) and use parallel DB2 software (licensed by IBM).  For more information on IMiner refer to IBM.

The functionality of Clementine and IMiner are almost identical.  Clementine has a nicer interface and is better in terms of visualisation, but is slower.

GeoMiner

GeoMiner claims to be a knowledge discovery system for spatial databases and GIS.  It is software implemented on a MapInfo proprietary GIS platform with access to on-line analytical processing functionality.  The available information regarding GeoMiner is hyped up containing exaggerated claims about its capabilities.  The functionality of the system is described using simple examples of the sorts of analysis that can be done with it.  The main spatial data mining operations are referred to as drill down and roll up.  Drill down is the process of examining data and mining results at higher general levels of spatial resolution, and roll up is the reverse process, which involves aggregating and generalising data and mining results at coarser levels of spatial resolution.

The GeoMiner functions include a geo-characterizer, a geo-comparator, a geo-classifier, a geo-associator, and a geo-cluster analyzer.  The geo-characterizer module is for finding ‘a set of characteristic rules at multiple levels of abstraction’.  Applying this module involves selecting and retrieving a subset of data from the database using some form of query.  Then some form of spatial aggregation is performed to group data into larger user defined regions.  Selected aspatial data variables are then analysed for each region using what is called the ‘attribute-oriented induction technique’.  The geo-comparator module is for defining a set of comparison rules, which contrast the general features of different classes of the relevant sets of data in a database.  This compares one set of data, known as the target class, to other sets of data, known as contrasting classes.  The geo-associator module is said to find a ‘set of strong spatial-related association rules’.  A typical spatial association rule is in th form of IF A THEN B (s%, c%) where A and B are sets of spatial or nonspatial predicates, s is the support of the rule (the probability that A and B hold together among all the possible cases), and c is the confidence of the rule (the conditional probability that B is true under the condition of A).  This functionality is already proposed for SPIN.  Mining spatial association rules is similar to the process of analysing aspatial association rules.  The geo-cluster analyzer module is for finding clusters of points with relevant aspatial attributes.  It uses an algorithm called CLARANS to perform spatial clustering.  Basically, the spatial clustering module involves drawing a user defined number of convex polygons to represent spatial clusters of point data.  Analysis can then be done by generalising and comparing the point attributes of the polygons.  Additional analysis might involve repeating this for different expected numbers of clusters and examining differences between the polygons.  The geo-classifier moule uses a decision-tree induction method to classify a set of relevant data according to one of the aspatial attributes. The classification tree is then displayed and by clicking on any of the nodes of it a user can highlight corresponding regions on a linked map.

The GeoMiner system although limited in some ways does enhance ESDA capablities.  For a more comprehensive review of the functionality in GeoMiner refer to SPIN!-report D3 from Work Package 3.