Creating raster information from point, line and
area data
Introduction
In rasterising point, line and area data for spatial
analytical purposes there are ways to minimise the level of spatial bias
when creating location, distance, density and direction grids. Often it
may be worth creating all the various types of grids for a specific input
coverage and on the other hand sometimes only one is appropriate. Often
extra information can be provided by several types of density grids, these
are generally the most rich in spatial information and can therefore be
of the greatest utility in spatial analysis. If all four types of grids
are created from a particular coverage most of the spatial information
is preserved and can be reverse engineered in some way, (attempts at this
can provide useful uncertainty information and guide the selection of initial
rasterisation resolution). The resolution of the initial rasterisation
is the major factor effecting the data error or uncertainty propogation
in the resulting grids. Given sufficient data quality information usually
the resolution of the initial rasterisation can be chosen to compromise
the data error in the input data coverages to minimise the uncertainty
propogation as far as possible.
Rasterisation of point, line and area data to
produce location, distance, density or direction grids should be done in
projections which respectively minimise the spatial bias in the resulting
grids. For example, when producing distance grids it would be best to transform
the geographical input data into a distance preserving projection calculate
the distances and reproject the results into the analytical projection.
I would have liked to have done this for our analysis but this must be
left until later. For now I believe that the error propogation caused by
projection distortions will result in only a small effect on model output
uncertainty as their are larger uncertainties lurking elsewhere.
Direction grids of some variables (eg. the aspect
of the DEM) maybe useful in the landuse classification but it is hard to
see how they could be useful for socio-economic data interpolation. Distance
and location grids are useful and there creation is easy, the hard bit
is the density surfaces.
Creating density information
from points
This is relatively easy, ArcView has a kernel density
algorithm for point data. The need is only to select the range of the kernel
and whether to use a variable to weight the points within the kernel. Using
a kernel method as such it is hard to decide whether an equal area or a
distance preserving projection or a compromise between the two is most
appropriate. Below are some maps which show the effect of increasing the
kernel extent on weighted kernel density surfaces generated from World
City Population Database:
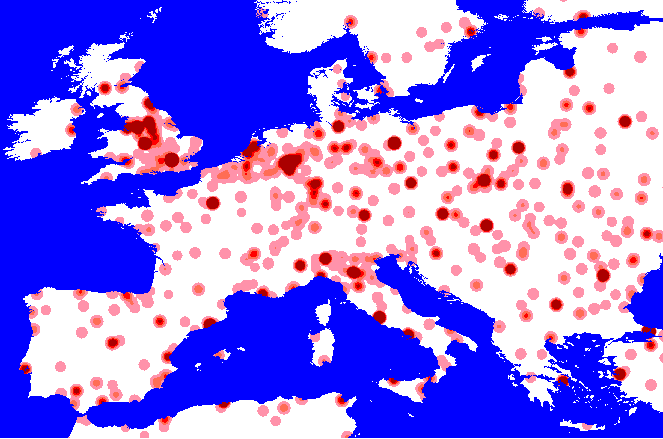
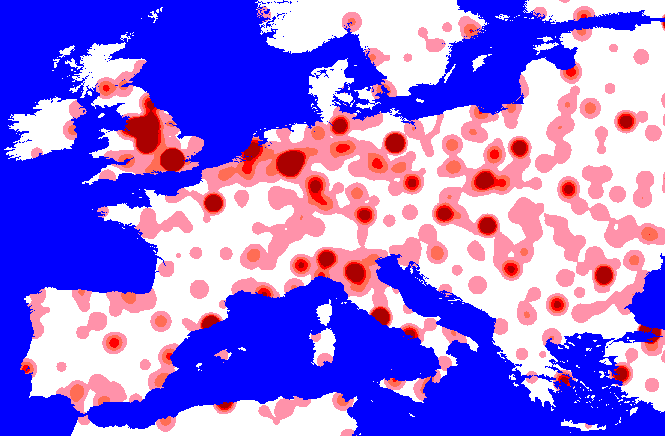
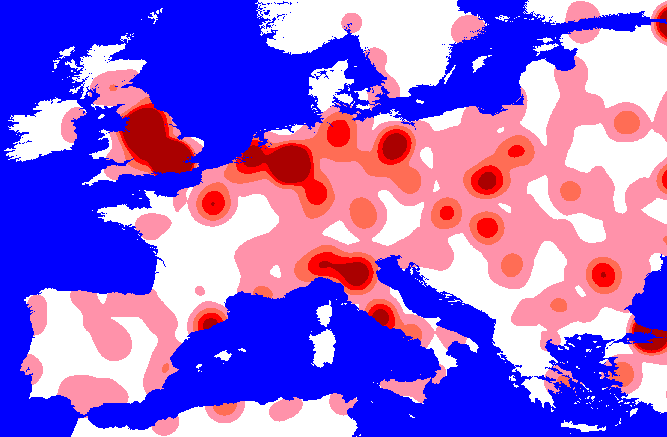
Creating
density information from lines
Line coverages from the DCW and Bartholomew data
sources were converted into density grids at a 1DM spatial resolution.
The problem of spatial biasing associated with rasterising line data can
be coped with by rasterising the lines at a detailed resolution and aggregating
up to the desired resolution in a spatially unbiased fashion. The method
developed to do this is outlined below with a specific example from the
DCW. The algorithm was applied to square rasters but would probably work
as well or better with triangular or hexagonal rasters. A spatially biased
density grid creation method had been used previously and the benefits
of using the spatially unbiased grids was not realised until Model 4 in
the population surface creation. The problem with creating these surfaces
using this method is it's computationally expensive and requires a large
amount of free disk space even if you employ tidy as you go database management.
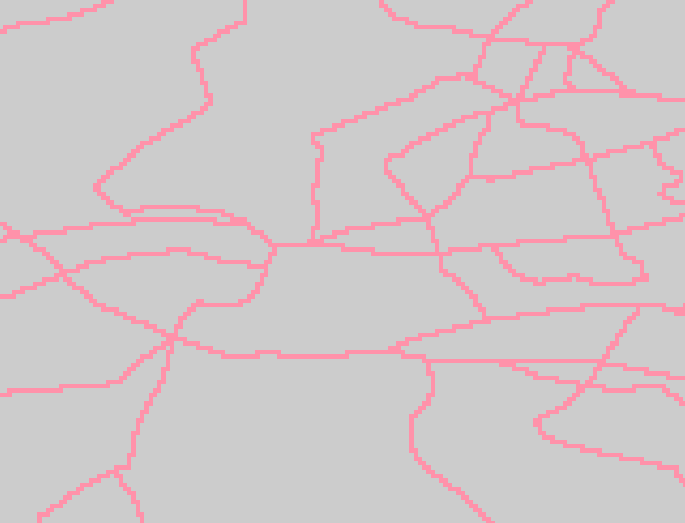
The lines shown below are part of the rdline coverage
from the DCW:
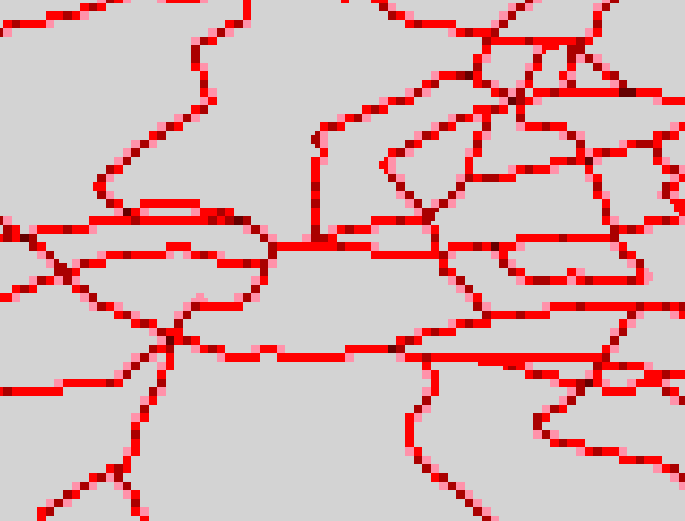
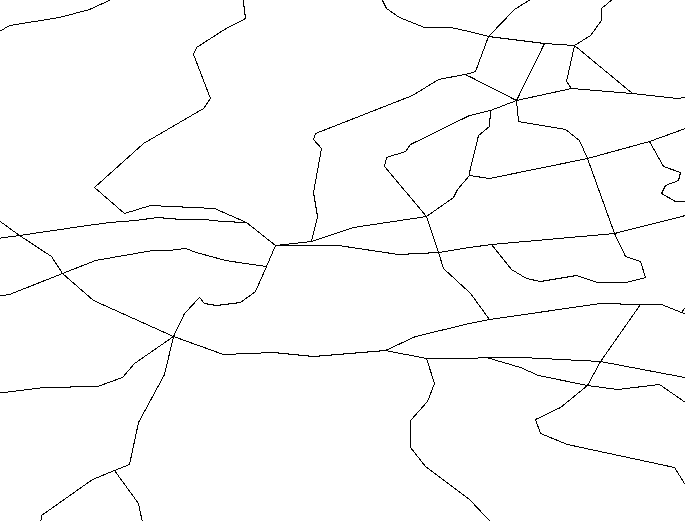Rasterising these lines at a 0.1DM resolution and
reclassing cell values so that cells containing road had value 1 and have
a value of 0 otherwise produces the grid shown below. This can be done
using; convert_to_grid then reclass in ArcView, or LINEGRID then RECLASS
in ArcInfo. (It would have been better if the initial rasterisation was
at 0.125DM resolution since (((0.125+0.125)+0.25)+0.5)=1 for reasons which
will hopefully become clear).
Aggregating the 0.1DM grid by a factor of 2 from
different nestings positions of the grid (opposite corners) produces the
grids are displayed below respectively. This can be done by using AGGREGATE
in ArcInfo, and GRIDCLIP (to remove the first row and column) then AGGREGATE.
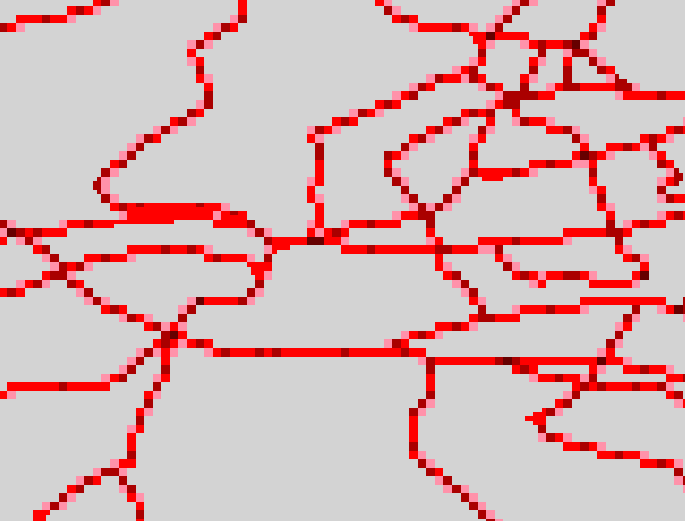The result of disaggregating the above grids back
to the initial raster resolution and adding them together is shown below.
This can be done using converting_to_ shapefile then convert_to_grid in
ArcView or GRIDPOLY then POLYGRID in ArcInfo.
Aggregating the summed grid to 0.2DM resolution produces
the following:
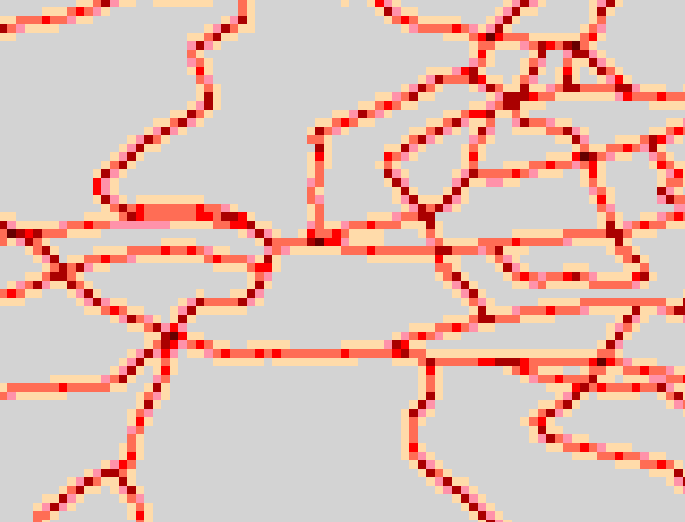This process of aggregating, clipping and aggregating,
dissagregating and summing, then reaggregating can continue until the desired
output resolution is attained. The algorithm can be summarised as follows:
-
Step 1 Rasterise data at an initial resolution
and reclass cell values
-
Step 2 Aggregate by factor of 2 from all corners
of the raster summing values
-
Step 3 Disaggregate the aggregate grids to
the resolution prior to aggregating in Step 2 and add together
-
Step 4 Aggregate by factor of 2
-
Step 5 Repeat steps 2 to 4 until data at desired
resolution.
The finer the initial resolution of the original
raster the smaller the rasterisation bias and the larger the range of density
values that will result. At Step 2 it is only necessary to do opposite
corners for square rasters.
The maps after the second iteration are as follows:
Iteraction 2 step 2;
Iteration 2 step 3;
Iteraction 2 step 4;
Iteraction 3 step 2;
Iteration 3 step 3;
Iteraction 3 step 4;
Iteraction 4 step 2;
Iteration 4 step 3;
Iteraction 3 step 4;
At iteration 2 step 4 in the example above the resolution is 0.8DM and
at iteration 3 step 4 the resolution is 1.6DM. To align the grids with
the other data for population modelling puposed we require a 1DM resolution
grid. To create the 1DM grid a compromise between these two resolutions
can be made. Converting the 0.8DM and 1.6DM resolution grids into shapefiles/polygon
coverages and converting back to grids of 1DM resolution, then since (1.6-1)/(1-0.8)=3
the 1DM grid based on the 0.8DM grid was multiplied by 3 and added to the
1DM grid based on the 1.6DM grid to produce the final output grid of rdline
density. Really this stage is quite unnecessary if the original rasterisation
resolution is appropriately chosen. The grid area for the same area shown
in the above maps and the map for the whole of Europe are shown below:
Creating
density information from areas
For areas basically the same procedure as for lines can be adopted again
based on the spatially unbiased kernel method. An example for urban area
polygon definitions from the DCW is given below. Starting with the polygons
shown below a 0.125DM, inside urban areas cells classed as 1 and 0 otherwise.
At the end of the first iteration the density surface shows a blurring
of the urban definition:
This blurring gets more pronounced at the end of iteration 2:
And yet more pronounced at the end of iteration 3:
Summing at the next level and disaggregating gives the following for this
chosen region (Manchester, Leeds, Brimingham):
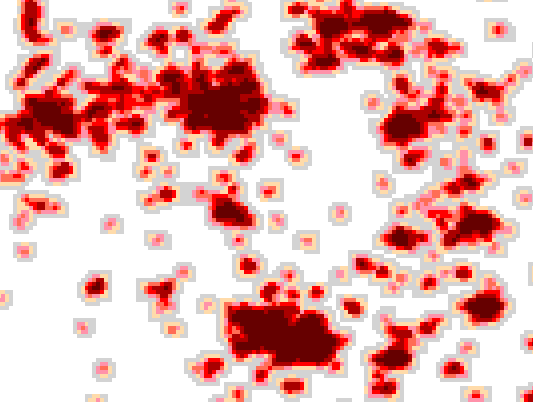
I think it is fairly obvious that this data will add better information,
this is what we used before in the location and cost distance grids:
An EU map may help convince you:
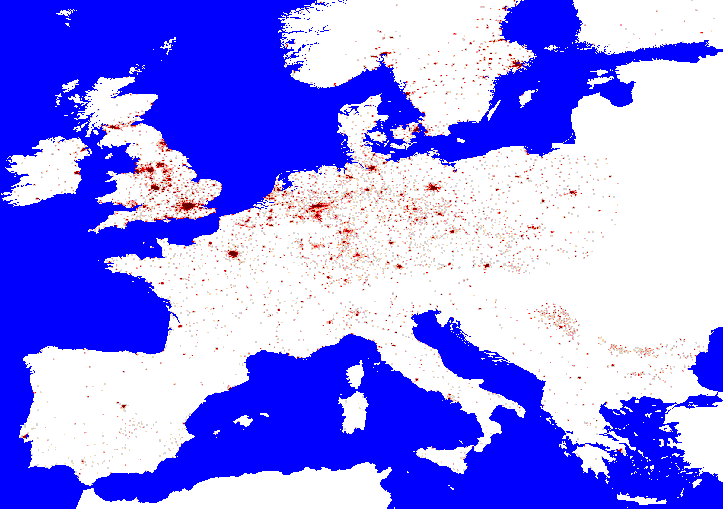At some level of aggregation the density layer may converge on the cost
distance layer!
Comments
In Models 1, 2 and 3 some spatially biassed line density grids based on
Bartholomew data were partially based on higher level aggregations than
this, and this may also be appropriate here. Hopefully now you see the
benefits of choosing an intitial rasterisation which is some nth root Initially
For now it is important to get aggregations at higher levels to much greater
than this to
All the above maps show values of each grid each classed seperately
into 7 categories using ArcViews natural break algorithm.
There can be a problem of lack of disc space when processing large relatively
dense line datasets. Despite as the resolution of the density grid gets
less detailed it takes less space to store, there are more values in the
grid and the space needed to store the shapefile or polygon coverage at
step 3 maybe huge. There are several ways of overcoming this problem:
-
The grid values can be reclassed so there are fewer resulting shapes/polygons;
-
the original raster can be split into smaller bits in the first place and
the resulting density grid at a 1DM resolution can be meshed or mosaiced
together; or,
-
At the iteration of the algorithm when the shapefile/polygon coverage begins
to get too big, the grid can be split into bits to create the shapefiles/polygon
coverages and make the diaggregate grids one at a time.
1 and 2 have problems associated with loss of information and edge effects
and for 3 you may eventually after hours of effort discover that you were
over optimistic in that the original raster was too high a resolution for
you to cope with.
There are other spatially unbiased methods for creating the density
grids. One alternative strategy is to create the initial raster at a 0.1DM
resolution in the same way then aggregate by a factor
of 10 from all intersecting points on the raster, disaggregate the results
to a 1DM resolution and add them all together. Using tidy as you go data
management this may take less space to do as the grid sumation doesn't
need doing all at the same time. The most appropriate method depends on
the data and what it will be used for.
With an appropriate initial rasterisation resolution it is easy to create
kernel density surfaces of lines going beyond the analysis resolution.
As yet the benefits of using such spatially unbiased density surfaces
in the population modelling are unclear. In Model_4
I plan to find out so both Bartholomew and DCW data density grids are being
calculated using the method outlined above. The proof of the pudding is
in the eating.